数据结构：突破基本类型的限制，存储更大的整数

任务

请你实现一个程序，输出 2 的 1000 次方的结果是多少。

思考

• C 语言中给我们提供的 int 类型，肯定是无法完成这个任务的，因为它表示不了这么大的数字。
• 用 long long 类型来进行解决，但long long 是 64 位整型，也就是占 64 个 2 进制位，它顶多能表示 2 的 64 次方减 1 的结果，相对于 2 的 1000 次方来说，小太多了。
• 用double类型进行解决，但存在一个严重的问题，就是 double 是有精度损失的。
  （double 的表示精度，一般来说是有效数字 15 位，就是一个数字，由左向右，从第一个不为零的数字起，向后 15 位都是准确的。因此 double 类型实际上也没有办法，准确表示 2 的 1000 次方的计算结果。）

那该怎么办呢？

编码解决

大整数表示法

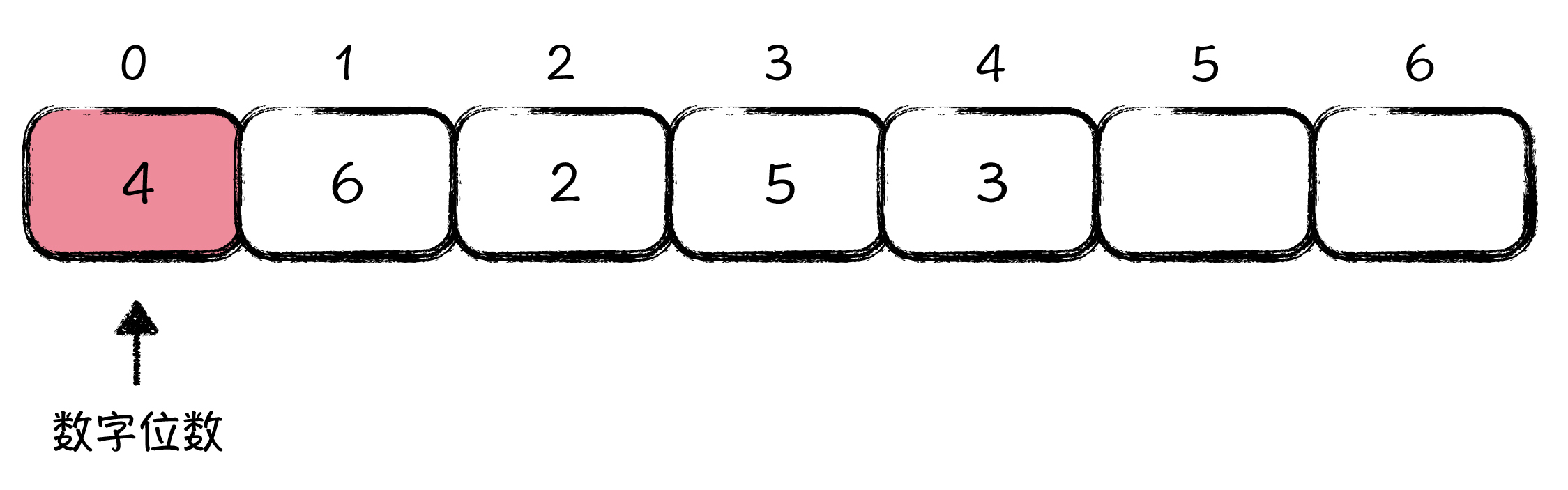
这种表示法中，使用数组的第 0 位存储数字的位数，因为 3526 有 4 位，所以数组的第 0 位就设置成了 4 这个值。接下来，数组从第 1 位到第 4 位记录的就是原数字 3526。

注意：这个数字是好像是倒着放置的，数字的最高位，也放在数组的最高位中。

如何计算大整数加法

计算 445 + 9667：

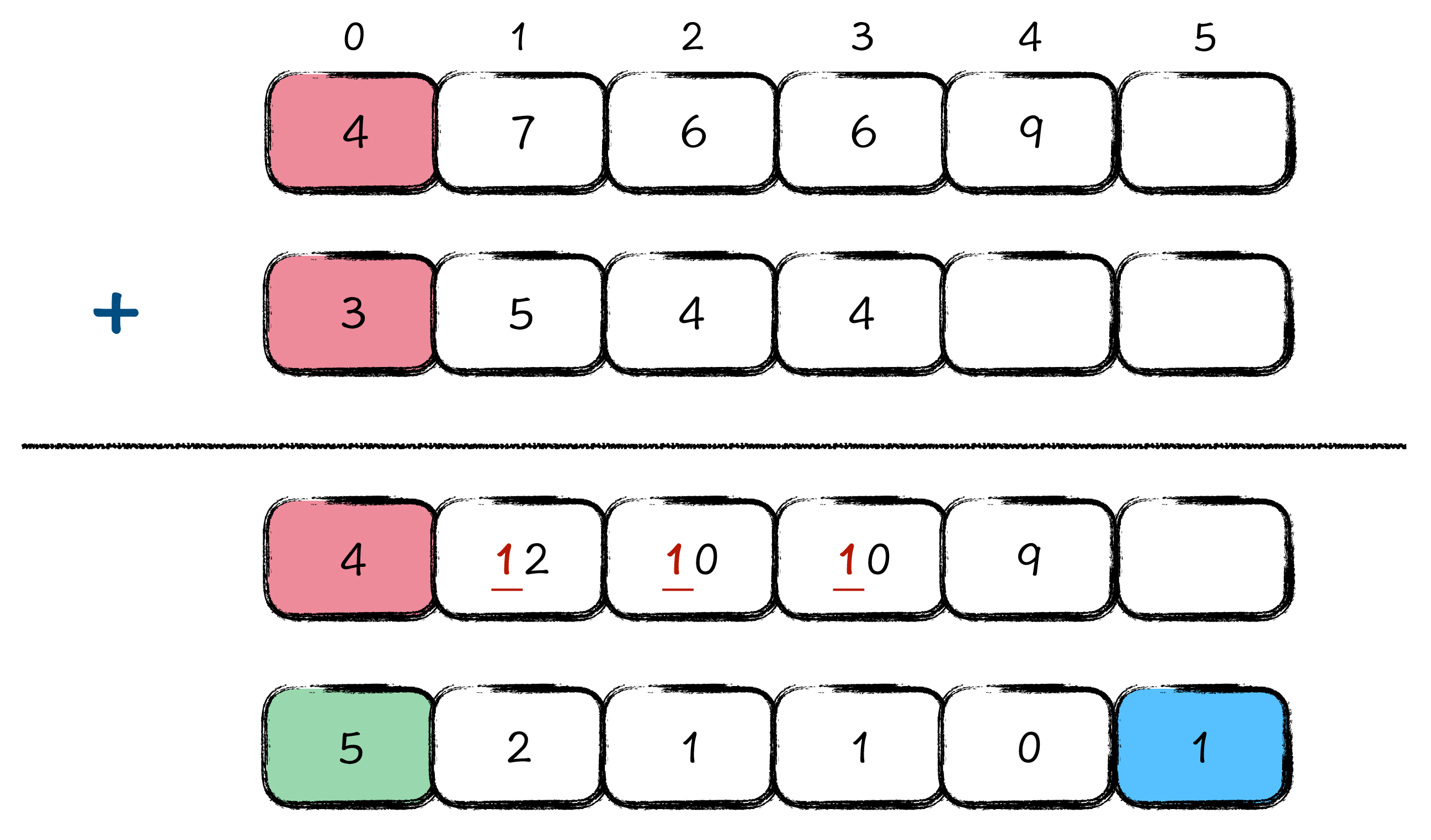
首先我们用大整数表示法，分别表示 445 和 9667 这两个数字；然后以位数最长的那个大整数，作为计算结果大整数的基础位数，445 和 9667 按位相加，得到一个 4 位的结果大整数，4 位分别是，9、10、10、12；最后我们再依次处理进位，就得到了底下那一行的结果：10112。

// 定义一个交换两个变量值的宏 swap
#define swap(a, b) { \
    __typeof(a) _t = a; \
    a = b, b = _t; \
}
// 实现大整数加法 a + b 的结果，存放在 c 中
void plus_big_integer(int *a, int *b, int *c) {
    // 让 a 指向位数较长的那个数字
    if (a[0] < b[0]) swap(a, b);
    // 大整数 c 的位数以 a 的位数为基准
    c[0] = a[0];
    // 循环模拟按位做加法
    for (int i = 1; i <= a[0]; i++) {
        if (i <= b[0]) c[i] = a[i] + b[i];      
        else c[i] = a[i];
    }
    // 处理每一位的进位过程
    for (int i = 1; i <= c[0]; i++) {
        if (c[i] < 10) continue;
        // 判断是不是最高位产生了进位
        // 如果是最高位产生进位，就进行初始化
        if (i == c[0]) c[++c[0]] = 0;
        c[i + 1] += c[i] / 10;
        c[i] %= 10;
    }
    return ;
}

实现

要计算 2 的 1000 次方的结果，就是要计算 1000 次乘法，最终的结果由于数值太大，我们肯定要使用大整数表示法了，所以要想理解这个计算过程，我们还是得回到大整数表示法本身，所对应的数学模型理解上。

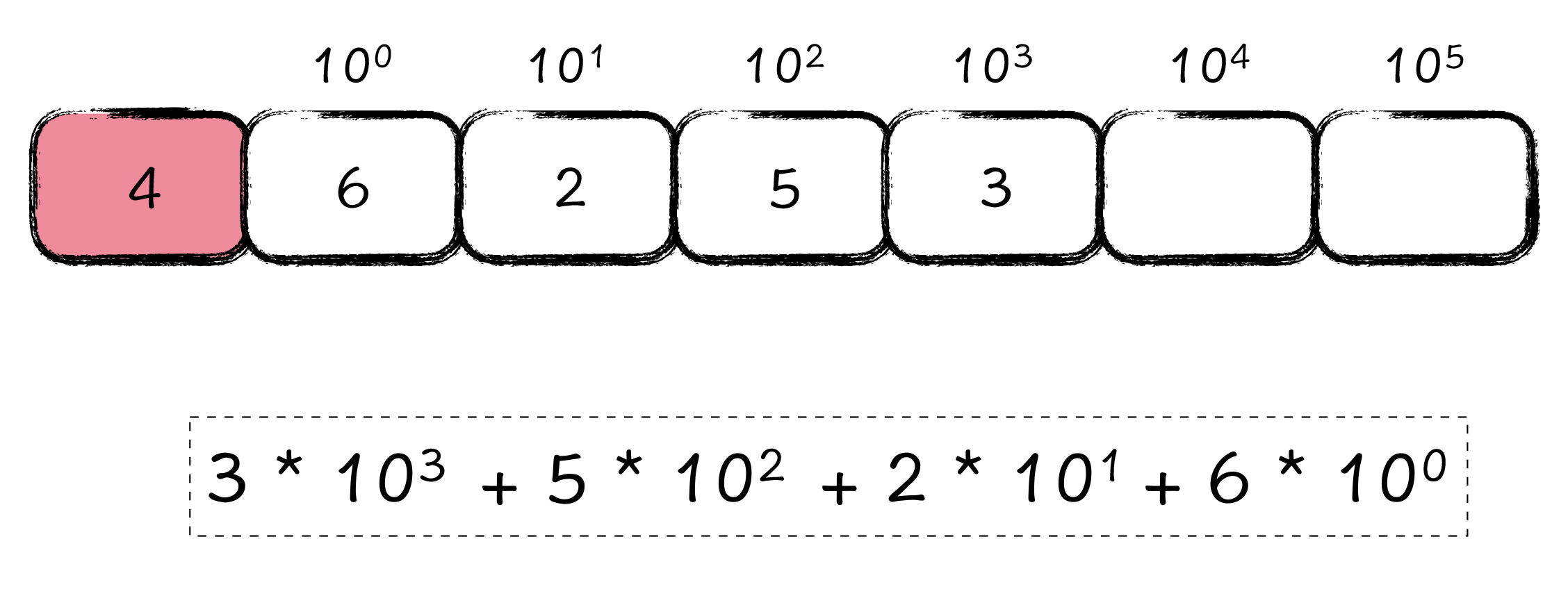
如上图所示，我们把大整数表示法中，每一个数字所对应的位权写出来，那么数组中所存储 3、5、2、6 的大整数信息，其实等价于下面的那一行数学公式，即 3∗10^3+5∗10^2+2∗10^1+6∗10^0。

我们对 3526 这个大整数乘以 2，其实等价于对下面那个数学式子乘以 2，就可以得到如下结果：

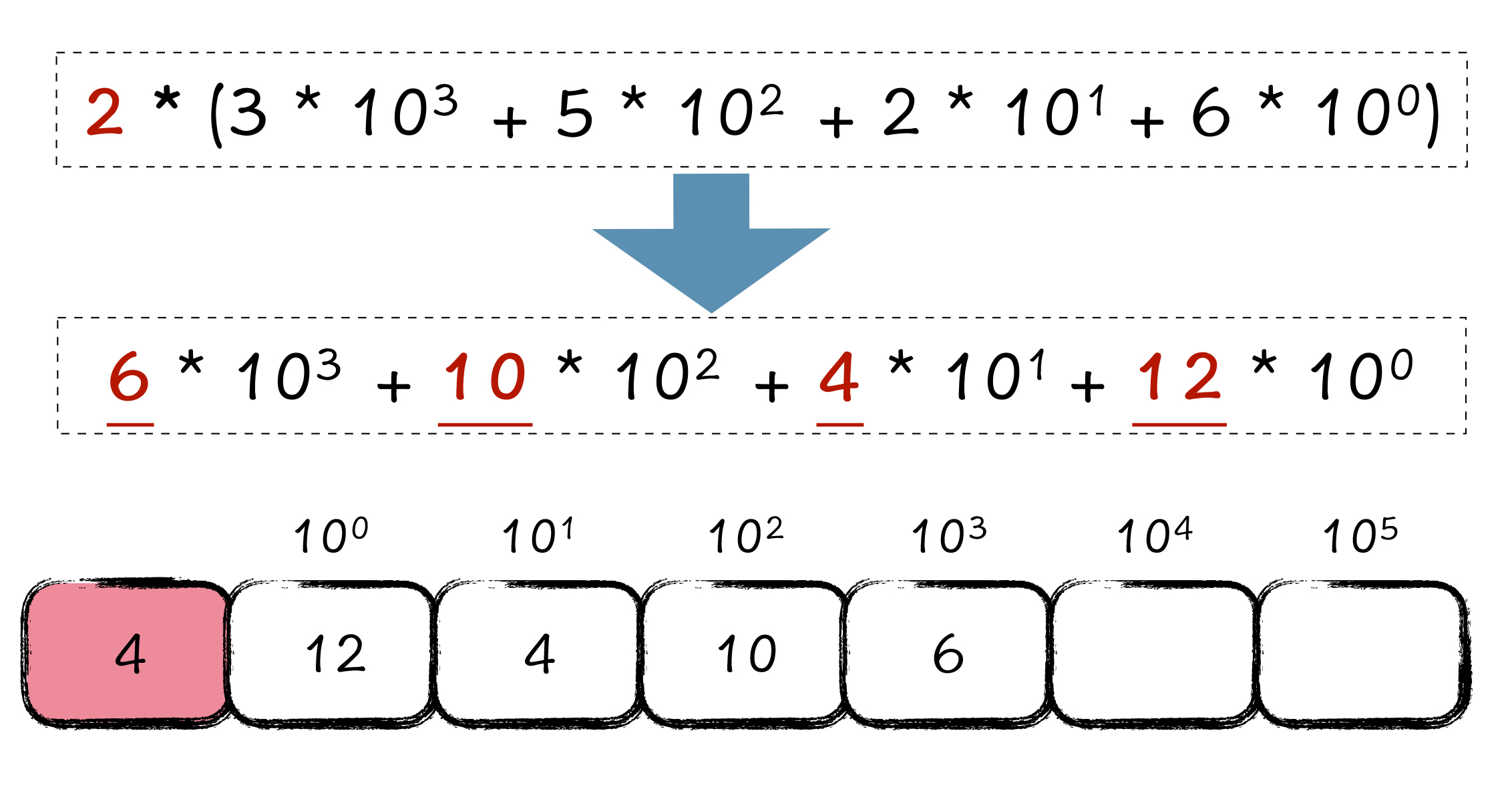
对某个大整数乘 2 的操作，其实，可以看成是对这个大整数的每一位分别乘以 2 的操作，然后再仿照大整数加法的过程，依次处理进位即可。

#include <stdio.h>

// 将 num 数组初始化成大整数表示的 1
// 作用就是做累乘变量
int num[400] = {1, 1}; 

int main() {
    // 计算 100 次 2 的 10 次方相乘的结果
    for (int i = 0; i < 100; i++) {
        // 对大整数的每一位乘以 2 的 10 次方
        for (int j = 1; j <= num[0]; j++) num[j] *= 1024;      
        // 处理进位
        for (int j = 1; j <= num[0]; j++) {
            if (num[j] < 10) continue;          
            if (j == num[0]) num[++num[0]] = 0;
            num[j + 1] += num[j] / 10;
            num[j] %= 10;
        }
    }
    // 输出大整数
    // 由于大整数是倒着存的，所以输出的时候倒着遍历
    for (int i = num[0]; i >= 1; --i) printf("%d", num[i]);
    printf("\n");
    return 0;
}

/**
 * 输出
 * 10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376/

小结

• 在大整数的表示法中，数字是从右到左，倒着存放在数组中的。
• 大整数的表示法，体现的是数据结构对于程序设计的作用。
• 大整数的加法和乘法过程，体现的则是算法对于程序设计的作用。
• 算法的底层是数学。
• 如果是计算流程不合理，我们需要改进算法；如果是数据表示受限，我们需要求助于数据结构。