二分查找：提升程序的查找效率

任务

假设你手上有 n 段长度不等的绳子，你现在想将这些绳子进行裁剪，裁剪出 k 条长度相等的绳子，注意，只能剪断绳子，不能拼接绳子。问题就是，你能得到的这 k 段绳子的最长长度是多长？

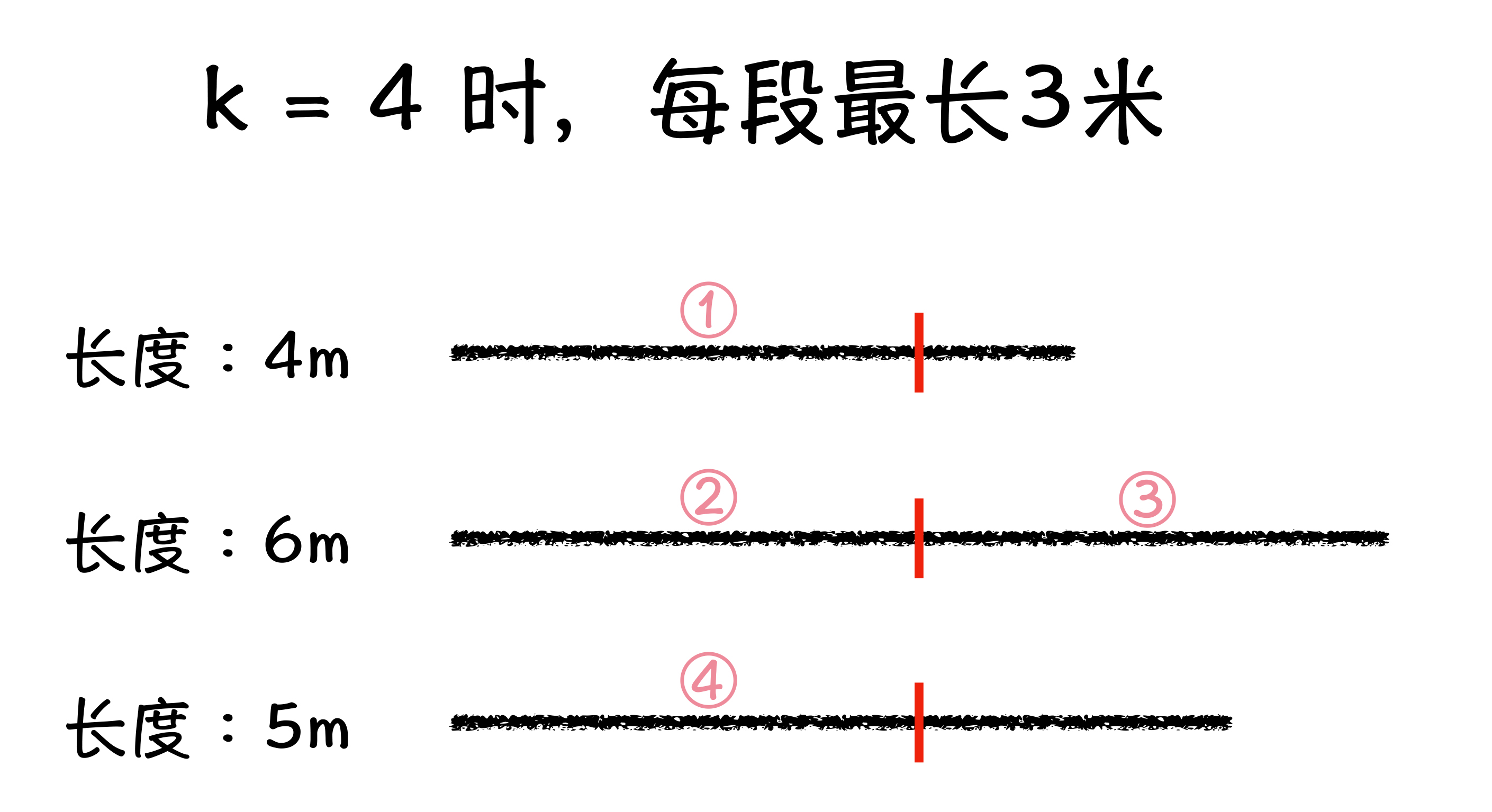
如图所示，如果你手中有 3 条绳子，分别是 4 米、6 米和 5 米，想要切出等长的 4 段，你会发现，每段最长就是 3 米。

思考

采用枚举法，就是先尝试能不能切出至少 4 段的 1 米长绳子，如果可以的话，再去尝试每段长度 2 米是否可行，依次尝试下去，直到尝试不下去为止。最后一次尝试可行的长度，就是每段绳子的最长长度了。（效率太低，放弃。）
采用二分法。

问题分析

二分法示例代码

中心思想：不管如何调整区间，都要保证待查找数字，总是落在我们的由 L 和 R 标记的查找区间内部。

int binary_search(int *arr, int n, int x) {
    //入参：有序数组 arr，数组长度 n 和待查找数字 x
    int l = 0, r = n - 1, mid;
    while (l <= r) {  //查找区间不为空
        mid = (l + r) >> 1; //l 和 r 的值，计算得到一个中间位置的下标 mid 值     
        if (arr[mid] == x) return mid;  //比较 mid 位置的值与 x 的大小关系，从而确定区间调整策略。
        if (arr[mid] > x) r = mid - 1;  //如果 arr[mid] 大于 x，说明 x 值在区间的前半段，那么 mid 及 mid 位置以后的值，就不在下一次查找的范围之内了，我们就把区间的尾部位置 r 向前移动，移动到 mid - 1 位。
        else l = mid + 1;  //arr[mid] 小于 x 时候的调整策略与之类似
    }
    return -1;
}

编码实现

将每一段绳子的长度 x，与能切出来的绳子段数之间，看成一个映射关系，用函数 f(x) = y 来表示，代表每一段长度为 x 的情况下，最多能切出来 y 段绳子。
f 函数是一个单调函数，随着每一段长度的增加，能切出来的段数 y 是在减少的，而对于我们来说，就是要确定 y = k 时的 x 的最大值。

#define EPS 1e-7  //EPS 是一个宏，就是我们要控制的精度，一般控制在 10^−7 范围，两个值相差不到 10−7 的时候，我们就认为这两个浮点值相等。
double l[100], n;

//传入每一段的长度 x，返回最多能切多少段
int f(double x) {
    //变量 n 记录的是原始绳子的数量，l 数组记录的是每一段原始绳子的长度
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        cnt += (int)floor(l[i] / x);
    }
    return cnt;
}

double binary_search(double *l, double *r, int k) {
    if (r - l <= EPS) return r;  //递归程序的边界条件，是当 r - l 小于等于一个极小值的时候，就终止递归
    double mid = (l + r) / 2.0;
    if (f(mid) < k) return bs(l, mid, k);
    return bs(mid, r, k);
}

小结

二分算法框架，是求解具有单调性问题的利器。
二分算法，通常用来求解那些 f(x) = y 问题中，给定 y，求解 x 的问题。
数组和函数在思维层面，没有什么本质差别。