重新认识数据结构：链表结构和思维

任务

首先，我们定义一种数字名称，叫做“快乐数”。所谓快乐数就是经过有限次变换以后，等于 1 的数字。这个变换规则，给出一个非 1 的数字 a ，把它的位数拎出来，求各个位数的平方和，得到一个数字 b，如果数字 b 不是 1，那就对数字 b 的每一位数再做平方和，得到数字 c……经过不停的变换，确定最后能否得到 1。

例如，一开始的数字是 19，经过变换规则 12+92=82，得到数字 82；因为不是 1 ，所以接着做变换，就是 82+22=68，再做一次变换 62+82=100，最后一次做变换 12+02+02=1，得到了 1 以后，停止。

注：此题LeetCode链接

实现

思考

首先，我们知道，整型表示的最大值是 231−1，大约是 20 亿左右。
例如，从 19 开始，依次得到的是：82、68、100、1 这些数字。也就是说，从一个数字开始，按照快乐数的计算规则，会得到一串数字序列。这其中就蕴含着链表重要的结构思维：从当前节点，唯一映射到下一个节点。快乐数序列中的数字，就是链表中的节点，如果当前数字确定了，下一个数字也就是确定了的，就像数字 19，下一个肯定是数字 82，这种映射规则，就是链表节点之间的指向关系。
思维映射：所谓快乐数序列，最终的目标是能到 1，这个数字 1，其实就可以看成是链表中的空地址。
在整型范围内解决快乐数问题的话，1999999999 这个数字，按照各位平方和来进行计算，得到的下一个数字应该是 (9∗9^2+1)=730————>这个快乐数链表中，节点数量绝对不会超过 731 个。一个不超过 731 个节点的链表，还总也走不到末尾，说明这个链表中有环。
因此，判断一个数字是否是快乐数，等价于判断链表中是否有环。

int hasCycle(struct Node *head) {
    if (head == NULL) return 0;
    // p 是慢指针，q 是快指针
    struct Node *p = head, *q = head;
    // 每次循环，p 走1步，q 走2步
    do {
        p = p->next;
        q = q->next;
        if (q == NULL) return 0;
        q = q->next;
    } while (p != q && q); 
    return p == q;
}

思考题

链表的操作

有如下函数接口定义：

1	struct Node erase(struct Node head, int ind);

请你参照链表插入操作，实现一个链表节点删除的操作，删除函数传入两个参数，分别代表指向链表头结点的指针变量 head，以及要删除的节点位置 ind，返回值代表删除节点以后的链表头结点地址。

代码

struct Node *erase(strcut Node *head, int ind) {
    struct Node ret, *p = &ret, *q;
    ret.next = head;
    while (ind--) p = p->next;
    q = p->next;
    p->next = p->next->next;
    return ret.next;
}

如何求解环的长度，如上图，环的长度就是5

如果链表中有环，那么采用快慢指针的方法，两个指针一定会在环中相遇。此时，可以让其中一个指针不动，另外一个指针再沿着环走一圈，直到两个指针再次相遇，这样，就能得到环的长度了。

如何找到环的起点，如上图，3号点就是环的起点

首先，假设从链表起始点到环的起点距离为 x，那么当快慢指针中的慢指针 p 刚刚走到环的起始点位置的时候，q 指针应该在环内部距离环起始点 x 的位置上，如图所示：

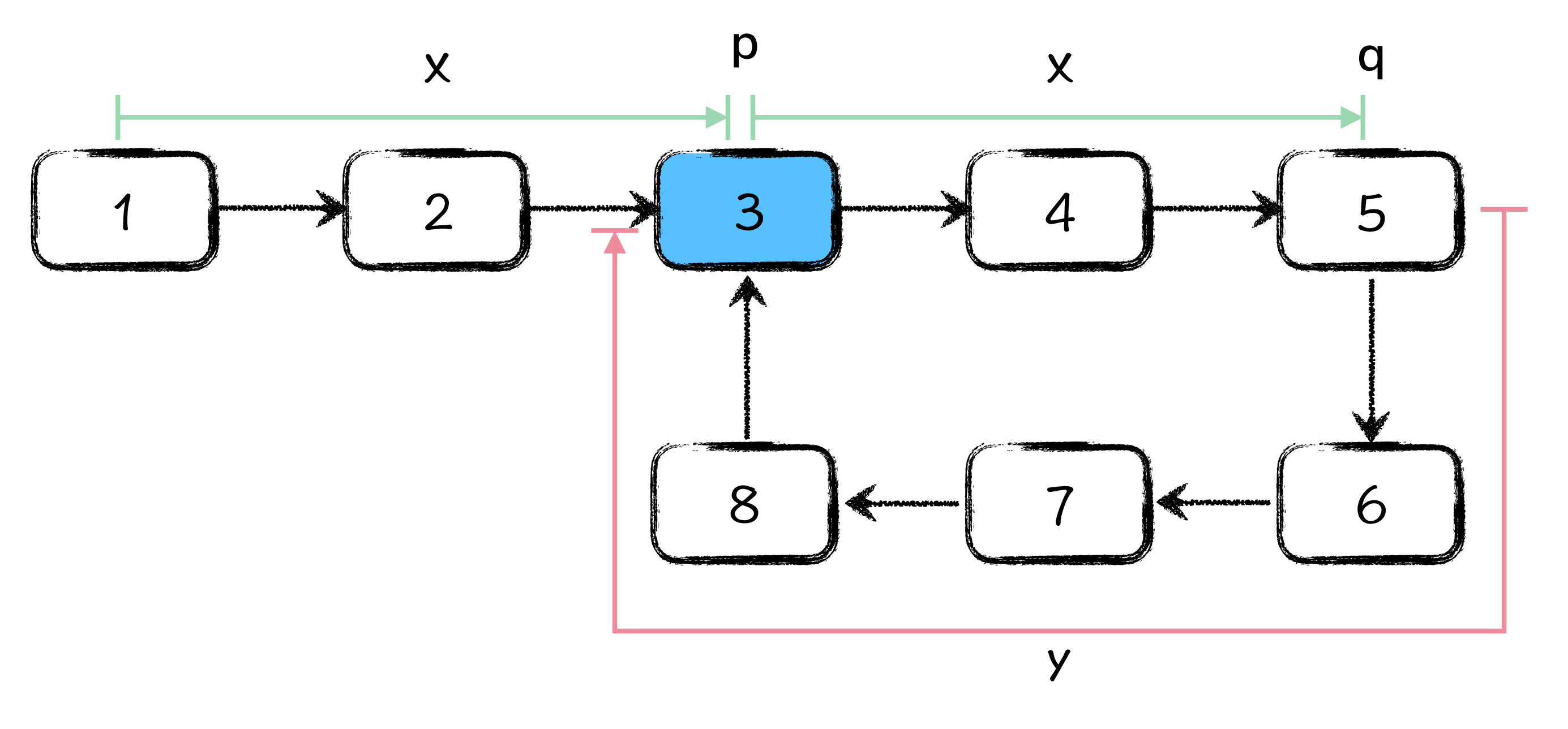
图中，q 指针距离环起始点 x 步，q 指针沿着链表向前走 y 步，就又可以到达环的起始点位置，如图所示 x + y 等于环长。也就是说，q 指针想要遇到 p 指针，就必须要追上 y 步的距离，又因为 p 指针每次走 1 步，q 指针每轮走 2 步，所以 q 指针每轮追上 1 步，也就是说，从此刻开始，当 q 指针追上 p 指针的时候，p 指针正好向前走了 y 步，如图所示：

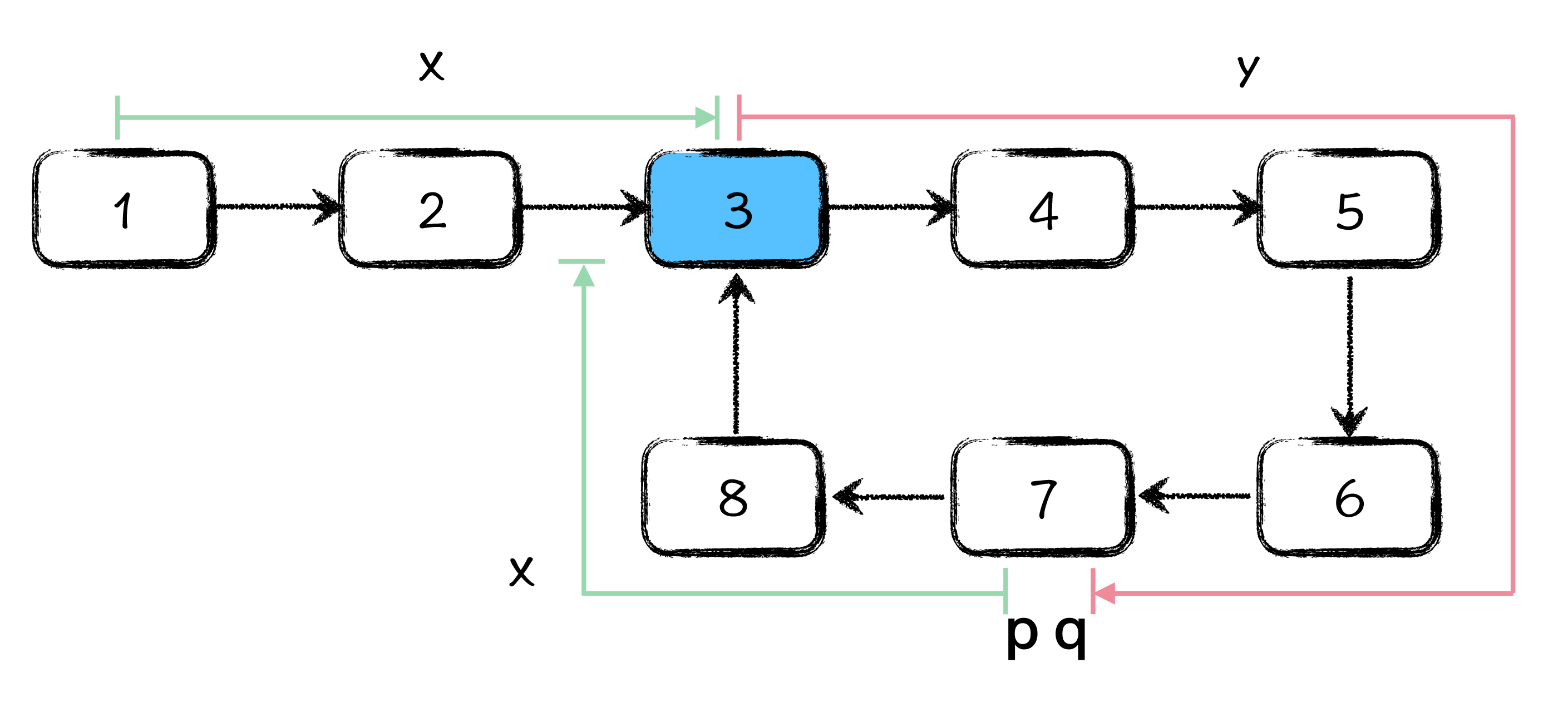
此时，你会发现 p 点在环中走了 y 步以后，p 和 q 相遇了，也就意味着 p 点再走 x 步就到环的起始点了。而恰巧，从链表头结点开始到环的起始点也是 x 步，所以此时只需要让 p 站在相遇点，q 指针回到链表的起始点，然后两个指针以相同的速度，一起往后走，直到二者再次相遇的时候，相遇点就是环的起始点了。

小结

数据结构 = 结构定义 + 结构操作，这个等式说明了我们学习数据结构的方法顺序。
单向链表节点中，存在数据域和指针域，指针域控制了链表的结构，一般不会根据应用场景的变化而变化，而数据域是根据应用场景的需求而设计的。