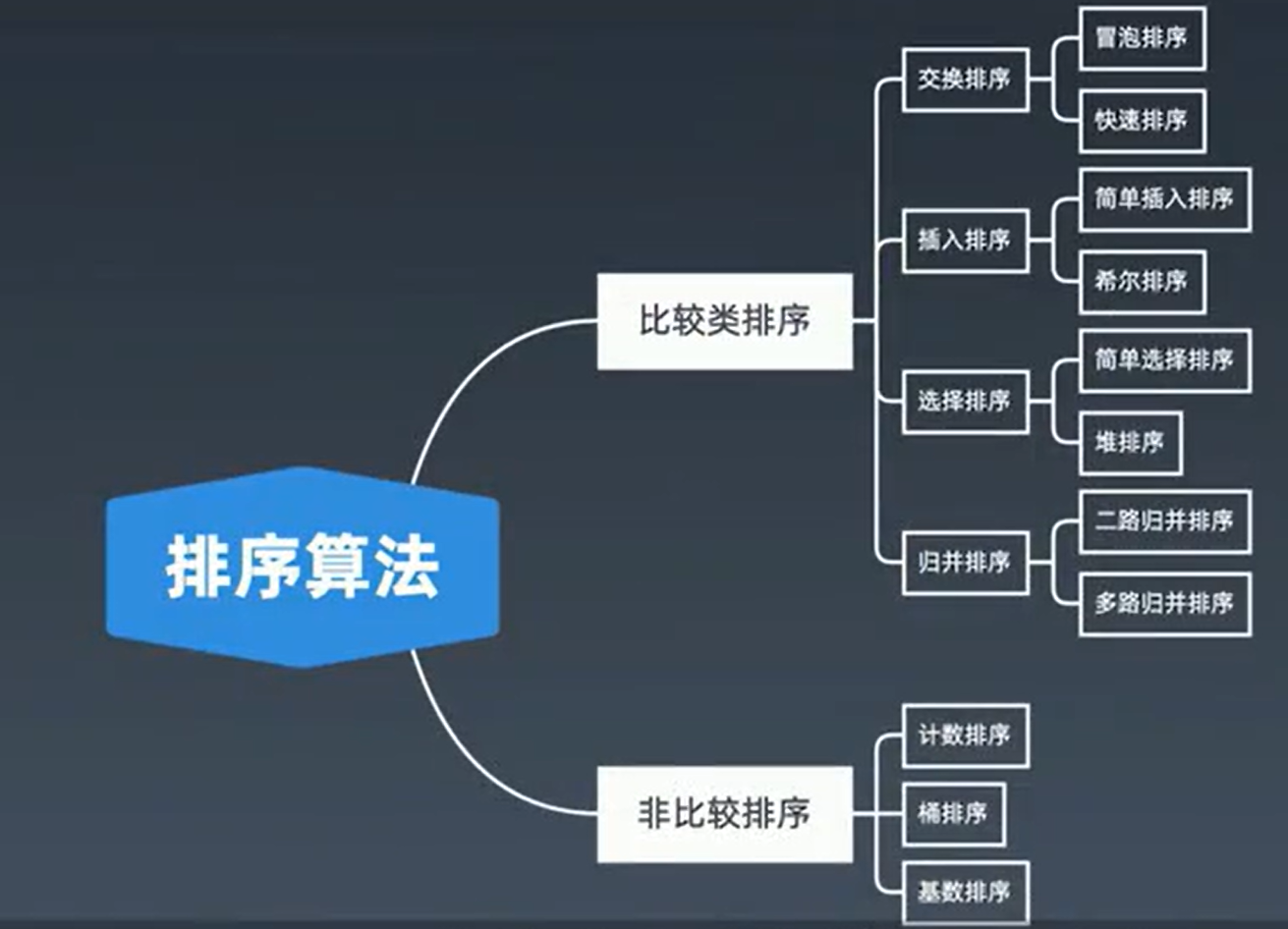
排序算法
1,比较类排序
通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
2,非比较类排序
不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
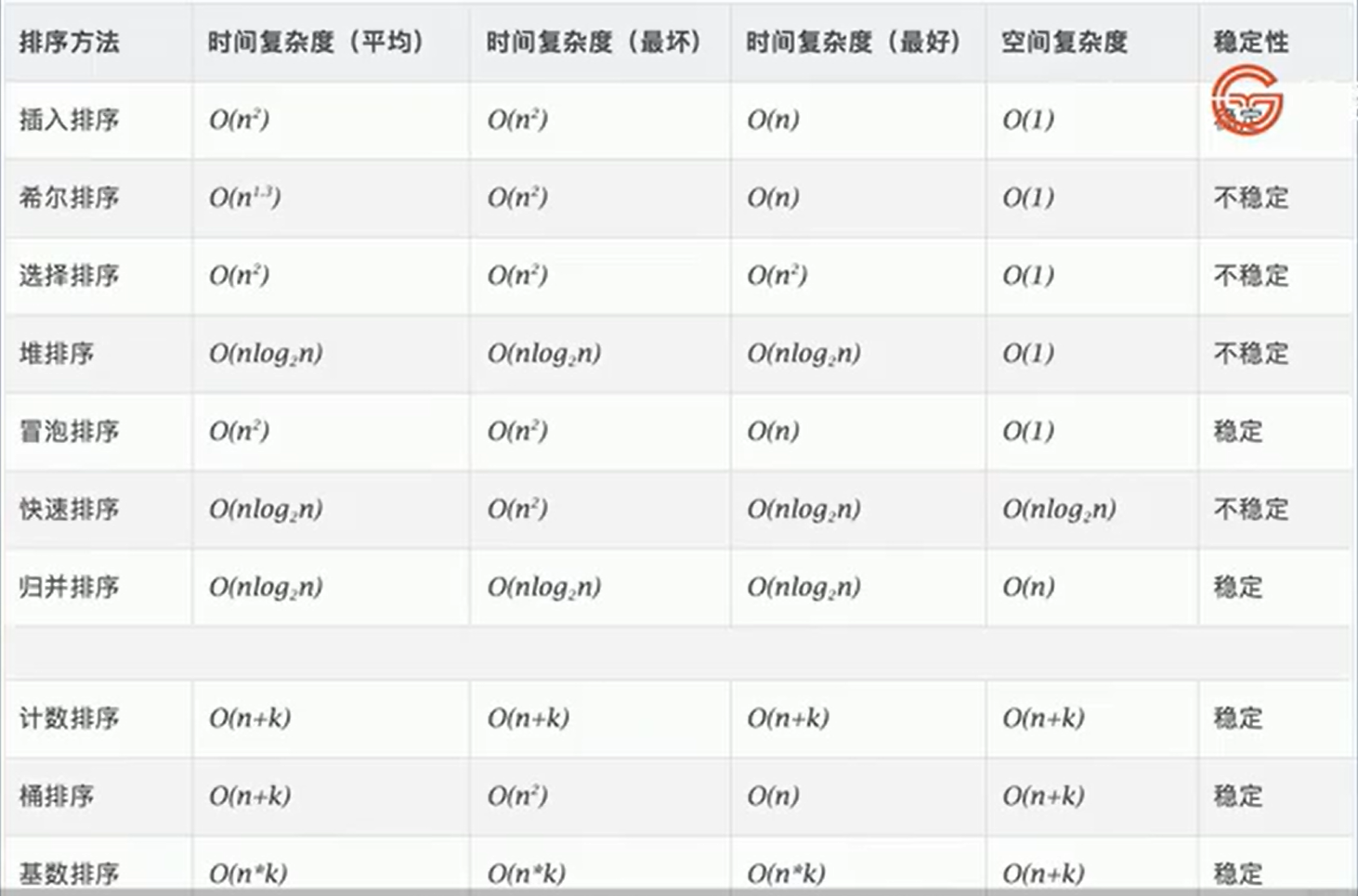
(大厂一般回考时间复杂度为nlogn的排序算法——堆排序、快速排序、归并排序,比如快速排序和归并排序用到了分治思想)
初级排序-O(n^2)
1,选择排序
每次找最小值,然后放到待排序数组的起始位置。
2,插入排序
从前往后逐步构建有序序列;对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
3,冒泡排序
嵌套循环,每次查看相邻的元素,如果逆序,则交换
高级排序-O(N*LogN)
- 快速排序
数组取标杆pivot,将小元素放pivot左边,大元素放右侧,然后依次对右边和右边的子数组继续快排,以达到整个序列有序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func quickSort(array []int, begin, end int) {
if end <= begin {
return
}
pivot := partition(array, begin, end)
quickSort(array, begin, pivot-1)
quickSort(array, pivot+1, end)
}
func partition(array []int, begin, end int) int {
pivot, counter := end, begin
for i := begin; i < end; i++ {
if array[i] < array[pivot] {
array[i], array[counter] = array[counter], array[i]
counter++
}
}
array[pivot], array[counter] = array[counter], array[pivot]
return counter
}
|
- 归并排序——分治
1,把长度为n的输入序列分成两个长度为n/2的子序列;
2,把这两个子序列分别采用归并排序;
3,将两个排序好的子序列合并成一个最终的排序序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public static void mergeSort(int[] array,int left,int right) {
if (right <= left) return;
int mid = (left + right) >> 1;
mergeSort(array,left,mid);
mergeSort(array,mid + 1,right);
merge(array,left,mid,right);
}
public static void merge(int[] arr,int left,int mid,int right) {
int[] temp = new int[right - left + 1];
}
|
小结
归并和快排具有相似性,但步骤顺序相反
归并:先排序左右子数组,然后合并两个有序子数组;
快排:先调配出左右子数组,然后对于左右子数组进行排序。
- 堆排序——堆插入O(logN),取最大/小值O(1)
1,数组元素依次建立小顶堆;
2,依次取堆顶元素,并删除。
链接
十大经典排序算法(动图演示)
快速排序算法示例
归并排序算法示例
堆排序代码示例



