题目链接
解法一:贪心算法
贪心算法,就是指它的每一步计算作出的都是在当前看起来最好的选择,也就是说它所作出的选择只是在某种意义上的局部最优选择,并不从整体最优考虑。
基本思路:
1,根据问题来建立数学模型,一般面试题会定义一个简单模型;
2,把待求解问题划分成若干个子问题,对每个子问题进行求解,得到子问题的局部最优解;
3,把子问题的局部最优解进行合并,得到最后基于局部最优解的一个解,即原问题的答案。
举例:我们从 c[0]=5, c[1]=3 且 k=11 的情况下寻求最少硬币数。按照“贪心原则”,我们先挑选面值最大的,即为 5 的硬币放入钱包。接着,还有 6 元待解(即 11-5 = 6)。这时,我们再次“贪心”,放入 5 元面值的硬币。
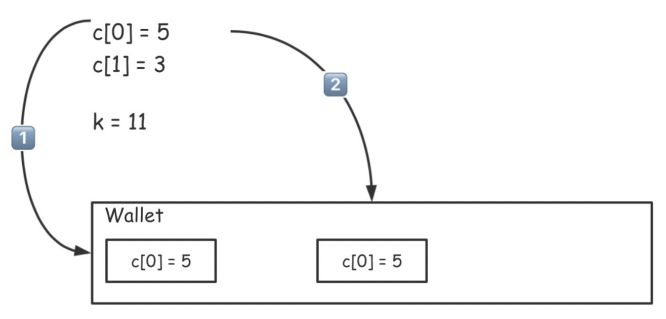
解法二:贪心算法的优化
解法三:动态规划
动态规划问题一定具备以下三个特征:
1,重叠子问题:在穷举的过程中(比如通过递归),存在重复计算的现象;
2,无后效性:子问题之间的依赖是单向性的,某阶段状态一旦确定,就不受后续决策的影响;
3,最优子结构:子问题之间必须相互独立,或者说后续的计算可以通过前面的状态推导出来。
当剩余的金额为 0 时结束穷举,因为这时不需要任何硬币就已经凑出目标金额了。在动态规划中,我们将其称之为初始化状态。
接着,我们按照上面提到的凑硬币的思路,找出子问题与原问题之间会发生变化的变量。原问题指定了硬币的面值,同时没有限定硬币的数量,因此它们俩无法作为“变量”。唯独剩余需要兑换的金额是变化的,因此在这个题目中,唯一的变量是目标兑换金额 k。在动态规划中,我们将其称之为状态参数。
接着,既然我们确定了状态,那么什么操作会改变状态,并让它不断逼近初始化状态呢?每当我们挑一枚硬币,用来凑零钱,就会改变状态。在动态规划中,我们将其称之为决策。
终于,我们构造了一个初始化状态 -> 确定状态参数 -> 设计决策的思路。
现在来写状态转移方程,通常情况下,状态转移方程的参数就是状态转移过程中的变量,即状态参数。而函数的返回值就是答案,在这里是最少兑换的硬币数。
1 | DP(values, k) { |
顺着这个思路,我把状态转移方程给写出来,它是这样的:

1 | //Go |
执行结果:通过
1 | 执行用时:8 ms, 在所有 Go 提交中击败了92.64% 的用户 |
辨别一个算法问题是否该使用动态规划来解的五大特点
- 求最优解问题(最大值和最小值);
- 求可行性(True 或 False);
- 求方案总数;
- 数据结构不可排序(Unsortable);
- 算法不可使用交换(Non-swappable)。

