知识点
- 集合的基本知识的具体应用;
- 映射的初步知识;
- 有理数的基本性质;
- 无穷等比数列求和的方法;
- 有理数的局限性
无穷等比数列求和的方法
公比$q = a_n / a_n-1$
求和 $S_n = a_1 + a_1q^2 + a_1q^3 + … + a_n*q^n-1$ (1)式
两边同时乘以q,qS_n = a_1q^2 + a_1q^3 + … + a_nq^n-1 + a_n*q^n$ (2)式
令(2)式 - (1)式: qS_n - Sn = a_1q^n - a_1
S_n*(q-1) = a_1*(q^n - 1)
S_n = a_1*(q^n - 1) / q - 1
当 n -> 无穷大 ,q^n -> 0, S_n ≈ a_1*(0-1)/q - 1
S_n ≈ a_1 / 1- q

关于pai
3 < pai <3 + 1
3 + 0.1 < pai < 3 + 0.2
3 + 0.1 + 0.04 < pai < 3 + 0.1 + 0.05
.
.
.
不足近似数列 < pai < 过剩近似数列

区间套理论
用两个端点都是有理数的区间,去一层套一层,直至到极限的情况下,定义出一个实数。
注意
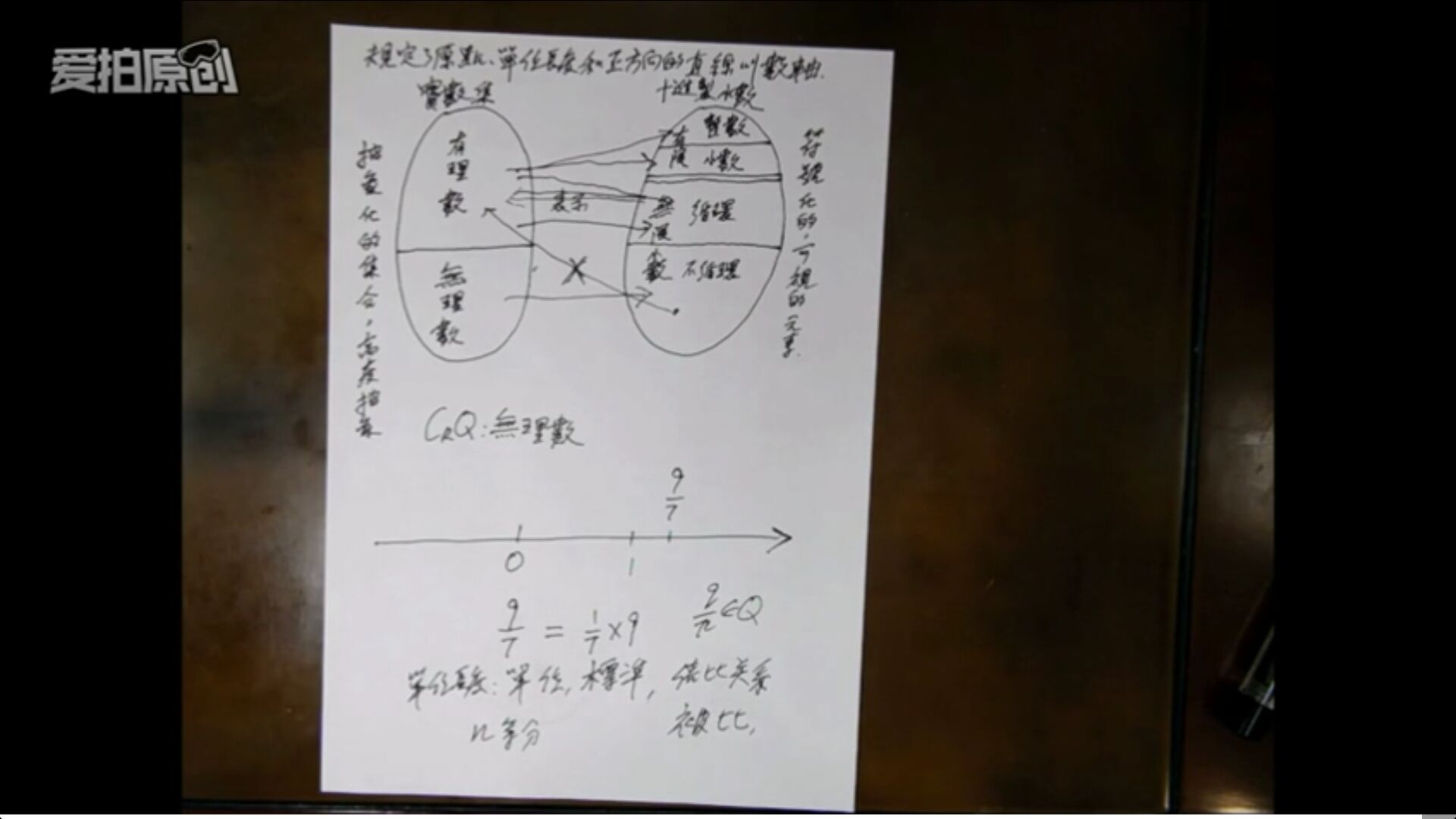
数轴是规定了原点,正方向和单位长度的直线
不是有理数的实数是无理数。
有限小数的补集 -> 无限小数
循环小数都是有理数
小节
本节收获了等比数列求和的推导过程(记得上高中那会这个公式可以出一道大题和一道选择或填空题);
对有理数和有理直线的定义。
数的范围,就像下面这张图
参考资料