队列与单调队列：滑动区间最大值

任务

滑动区间最大值，就是指在固定区间长度的前提下，在一个序列上，从前到后滑动这个区间窗口，每次窗口内部的最大值，就组成了滑动区间最大值。

例如，给你如下包含 8 个数字的序列，区间长度设置为 3：

[6 4 2] 10 3 8 5 9 -> 6
6 [4 2 10] 3 8 5 9 -> 10
6 4 [2 10 3] 8 5 9 -> 10
6 4 2 [10 3 8] 5 9 -> 10
6 4 2 10 [3 8 5] 9 -> 8
6 4 2 10 3 [8 5 9] -> 9

滑动区间从数字 6 开始出发，每次向右移动一个数字，同时把左边的一个数字丢出去，保持区间长度为 3，最后移动到数字 9 停止。可以看到，这个序列共包含 8 个数字，所以最后形成的滑动区间最大值共有 6 个，依次是 6、10、10、10、8、9。

常规解法：采用 O(nm) 的算法来完成，n 是区间长度，m 是窗口长度，就是枚举区间的终止位置，每次扫描区间内部，获得最大值。

要求解法：时间复杂度降低到 O(n)。

编码实现

初识队列

先到先得，先入先出，每个元素都是从队列尾部入队，在头部被处理完后再出队。如下图所示：

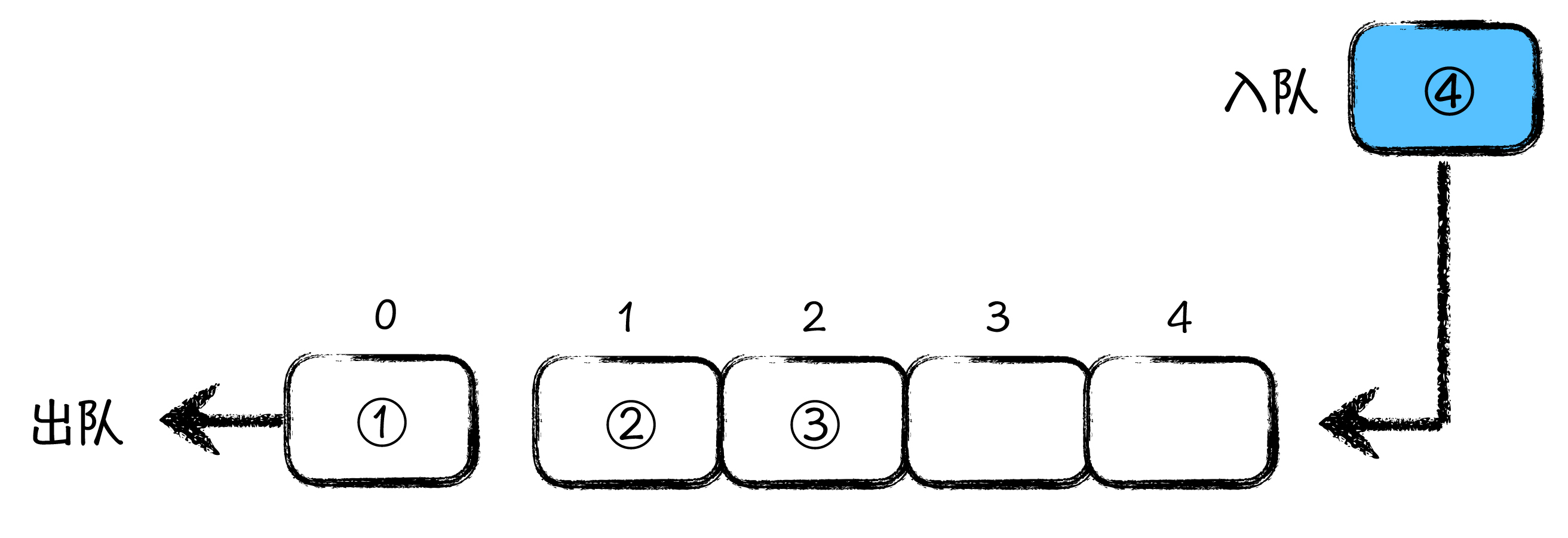
单调队列

单调队列的作用，就是用来维护在队列处理顺序中的区间最大值。维护的就是区间长度为 3 时候的最大值。当一个新的元素入队的时候，它会把其前面违反单调性的元素，都从队列中踢掉，最终将一直维护着一个最大值。

滑动区间最大值

本身就是求区间最大值的，所以也符合了单调队列应用的场景：维护在队列处理顺序中的区间最大值。

#define MAX_N 1000
int q[MAX_N + 5], head, tail;
void interval_max_number(int *a, int n, int m) {
    head = tail = 0;
    for (int i = 0; i < n; i++) {
        // a[i] 入队，将违反单调性的从队列 q 中踢出
        while (head < tail && a[q[tail - 1]] < a[i]) tail--;
        q[tail++] = i; // i 入队
        // 判断队列头部元素是否出了窗口范围
        if (i - m == q[head]) head++;
        // 输出区间内最大值
        if (i + 1 >= m) {
            printf("interval(%d, %d)", i - m + 1, i);
            printf(" = %d\n", a[q[head]]);
        }
    }
    return ;
}

函数内部，依次处理数组中的每个元素，每次处理相应元素的时候，涉及到两个过程：

第一个过程，是将当前元素入队。在入队之前，将队列尾部违反单调性的元素都从队列中踢出，这个就是第 7 行 while 过程的作用，之后就是将编号 i 入队即可。这里注意，单调队列里面，存储的是 a 数组的下标，而不是 a 数组的值。其实存储了下标，我们就可以索引到值，而在上一节二分查找的课里面，我们也见识过了，要是存储了值，想要反向索引下标是比较困难的。
第二个过程，就是判断单调队列头部的元素是否超出了窗口范围，也就是前面我们例子中你的学长毕业的过程，如果元素下标已经超出了窗口范围，就将队列头部元素出队。

这样就可以保证，我们每次输出的，就都是滑动窗口内部的区间最大值了。

小结

单调队列应用的场景：就是维护队列处理顺序中的区间最大值。
定义一种性质，并且维护这种性质。单调队列，维护的就是单调性。
单调队列处理单个元素的平均时间复杂度为什么是 O(1) 的。假设我们要处理 n 个元素，从整体上来看，每个元素会入队列 1 次，出队列最多也是 1 次，那么 n 个元素的总操作次数不会超过 2×n 次，平均到一个元素上就是 2 次，也就是常数次，记作 O(1) 时间复杂度。由此得知，处理 n 个元素的总时间复杂度，就是 O(n)。