极客时间_7天算法体验营_Day1-时间复杂度和空间复杂度分析

常见的7种时间复杂度

O(1)：常数复杂度；
O(log n)：对数复杂度；
O(n)：线性时间复杂度；
O(n^2)：平方；
O(n^3)：立方；
O(2^n)：指数；
O(n!)：阶乘法。

通过代码来分析时间复杂度(Golang)

O(1)

1 2	n := 100 fmt.Print(n)

程序只执行1次。

O(N)

1
2
3

for i:=1;i<=n;i++ {
    fmt.Println("hello:",i)
}

程序将fmt.Println("hello")执行了n次。

O(N^2)

for i:=1;i<=n;i++ {
    for j:=1;j<=n;j++ {
        fmt.Println("hello:",i,j)
    }
}

程序将fmt.Println("hello")执行力n*n=n^2次。

拓展：如果是以下代码，时间复杂度是多少？

for i:=1;i<=n;i++ {
    fmt.Println("hello:",i)
}

for j:=1;j<=n;j++ {
    fmt.Println("hello:",j)
}

因为两个循环是并列关系，所以fmt.Println("hello")被执行了2*n次，我们忽略常数系数，所以时间复杂度是O(N)。

总结：如果循环是N层嵌套关系，则时间复杂度是O(N^N)，如果循环是并列关系，则时间复杂度是O(N)。

O(log(n))

1
2
3

for i:=1;i<n;i=i*2 {
    fmt.Println("hello:,"i)
}

O(k^n)

func fib(n int)int {
    if n < 2 {
        return n
    } else {
        return fib(n-1) + fib(n-2)
    }
}

这是一个递归程序。

时间复杂度曲线图

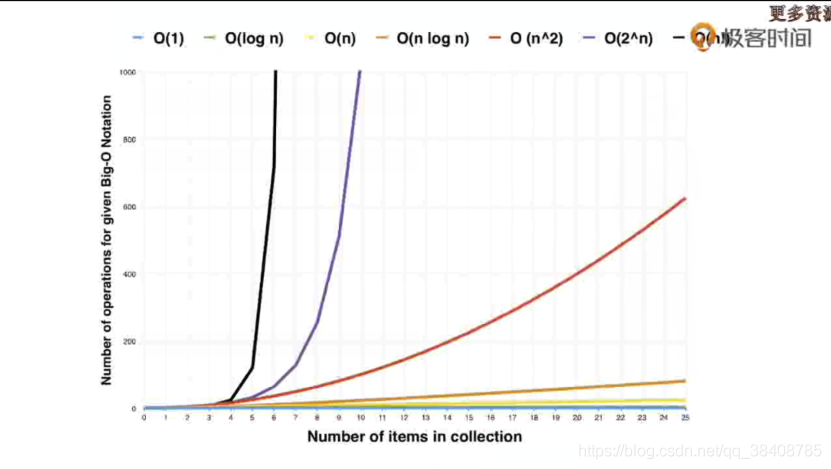
一定要在写程序的时候时刻考虑时间复杂度；
能够用最简单的时间复杂度和空间复杂度完成这段程序的话基本是一个顶尖职业选手的必备素养。

例题

计算1+2+3+…+n

方法一：循环

1
2
3

y = 0
for i = 1 to n:
    y += i

时间复杂度O(n)

方法二：求和公式

1	y = n * (n + 1) / 2

时间复杂度O(1)

求斐波那契数列第n项和

func fib(n int)int {
    if n < 2 {
        return n
    } else {
        return fib(n-1) + fib(n-2)
    }
}

画出递归树分析时间复杂度：

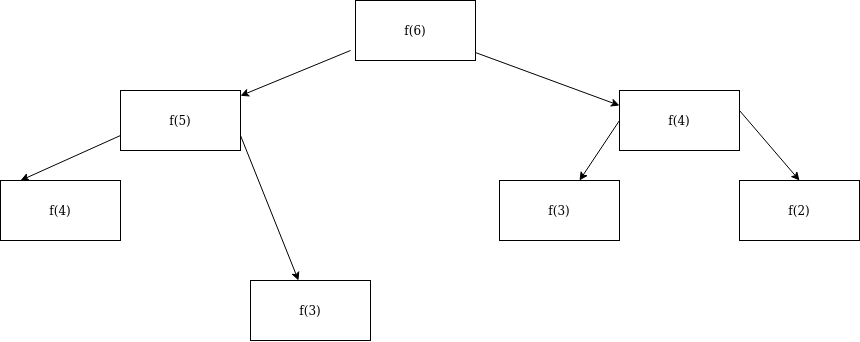
主定理（重要）

思考题

二叉树遍历-前序、中序、后序：时间复杂度是多少？
图的遍历：时间复杂度是多少？
搜索算法：DFS、BFS时间复杂度是多少？
二分查找：时间复杂度是多少？

面试四件套

１，和面试官沟通清楚问题，扫清问题的盲点；
２，想所有可能的解决方案；
３，比较时间和空间复杂度，找出最优解；
４，写程序实现；
５，测试结果。

空间复杂度

通过亮点来分析：

数组的长度
递归的深度（特殊说明）

实例分析

https://leetcode-cn.com/problems/climbing-stairs/solution/

小结

常用工具配置
基本功和编程功法
常见的时间、空间复杂度

个人感受

我最开始体会到时间复杂度的优势是在大二参加算法竞赛前夕，犹记得在搜索某一个算法题目的题解的时候，眼睁睁看着作者将一段复杂的程序通过微积分优化成一行简易的代码，AC一遍直接通过，这使我留下了时刻的印象。
工作后虽然我主要做的是开发，但有些优化时间复杂度的思想有时也会用在业务逻辑中，希望我后期可以最简单的时间复杂度和空间复杂度完成一段程序，达到职业选手的素养！

链接

知乎_如何理解算法时间复杂度的表示法，例如 O(n²)、O(n)、O(1)、O(nlogn) 等？