算法训练营-Trie树、并查集的基本实现和特性

复习

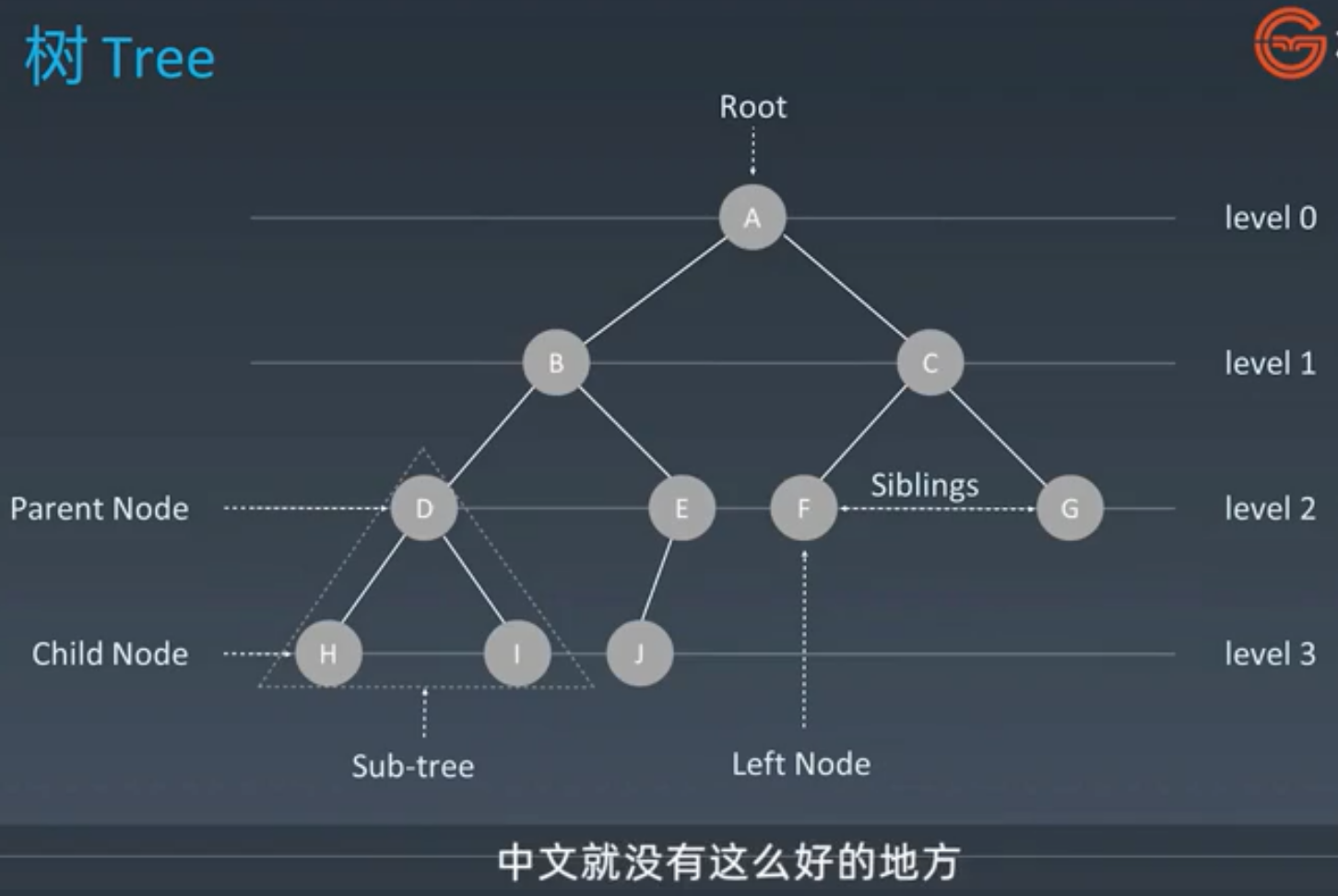
树

• 前序(Pre-order)：根-左-右
• 中序(In-order)：左-根-右
• 后序(Post-order)：左-右-根

记忆方法：前序->根在最前面，中序->根在中间，后序->根在最后，左永远在右的前面。

示例代码

def preorder(self,root):
    if root:
        self.traverse_path.append(root.val)
        self.preorder(root.left)
        self.preorder(root.right)

def inorder(self,root):
    if root:
        self.inorder(root.left)
        self.traverse_path.append(root.val)
        selft.inorder(root.right)

def postorder(self,root):
    if root:
        self.postorder(root.left)
        self.postorder(root.right)
        self.traverse_path.append(root.val)

二叉搜索树

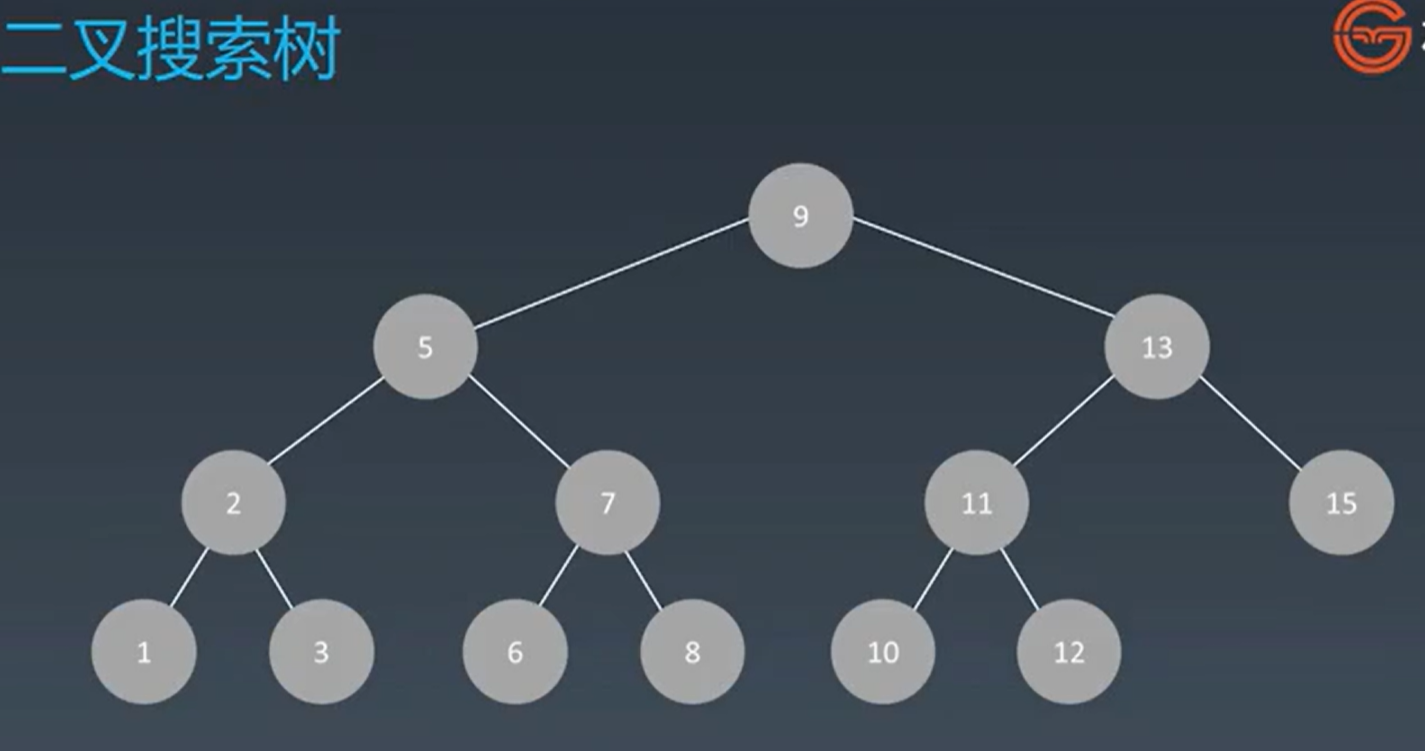
是子树的关系，并不是儿子和父亲的关系。
定义：任何一个结点，它的左子树的所有的结点都要小于这个根结点，它的右子树的所有结点都要大于根结点，且对于它的任何子树同样地以此类推，对于任何子树都满足这样的特性。
另外一个特性：二叉搜索树是一个升序的序列。

极端情况（链表）

思考：如何平衡？

字典树

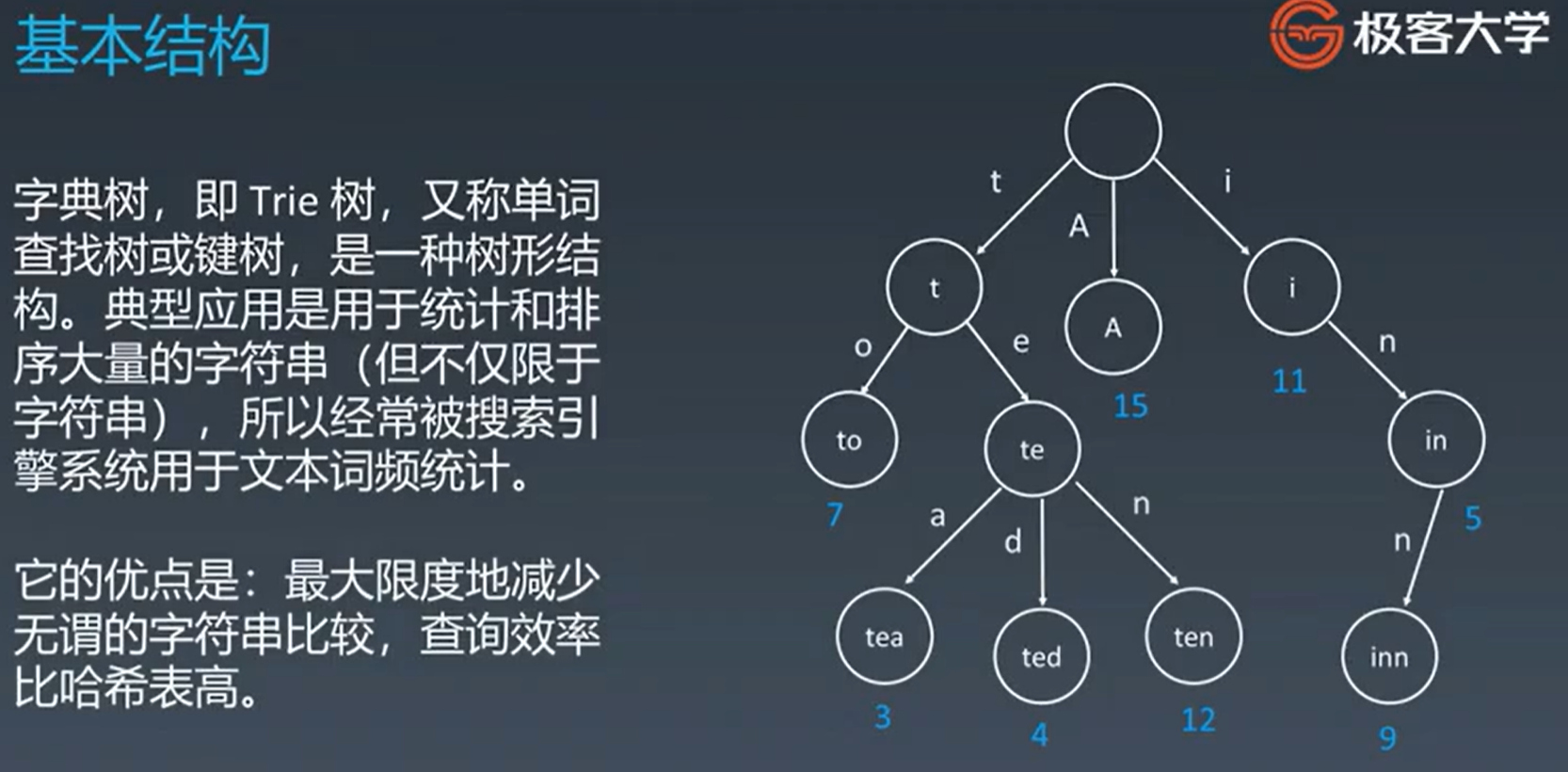
基本性质

• 1，结点本身不存在完整单词
• 2，从根结点到某一结点，路径上经过的
• 3，每个结点的所有子结点路径代表的字符都不相同

结点的内部实现

核心思想

Trie树的核心思想是空间换时间
利用字符串的公共前缀来降低查询的时间的开销以达到提高效率的目的

相关题目解析

leetcode-208.实现Trie