AVL树
- 发明者:Adelson-Velsky and Landis Tree
- Blance Factor(平衡因子):是它的左子树的高度减去它的右子树的高度(有时相反)。balance factor= {-1,0,1}
- 通过旋转操作来进行平衡(四种)
- Self-balancing binary search tree
- 不足:结点需要存储额外信息、且调整次数频繁
记录左右子树高度
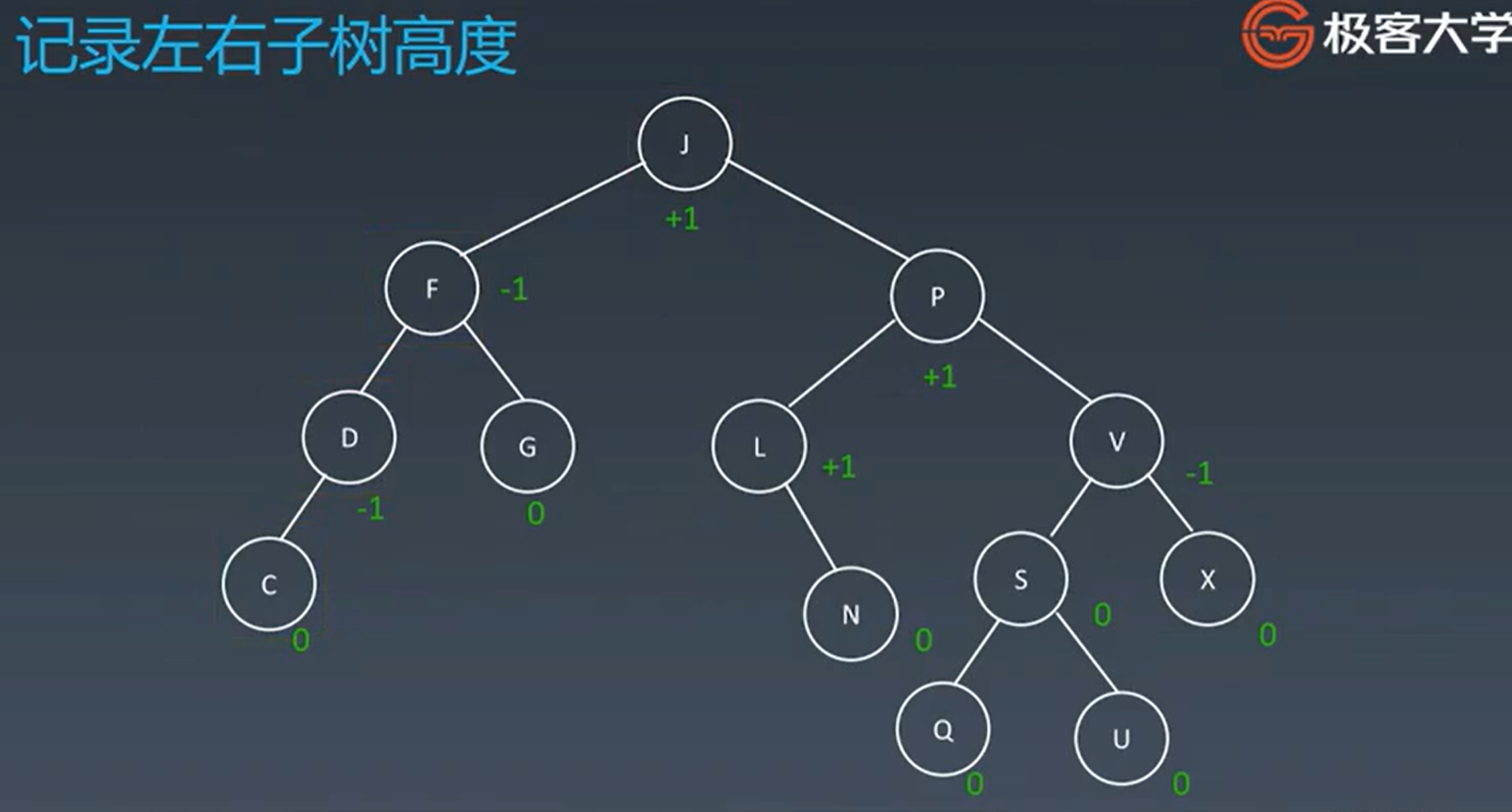
例如F点,右子树高度1 - 左子树高度2 = -1
旋转操作
1,左旋

2,右旋

3,左右旋
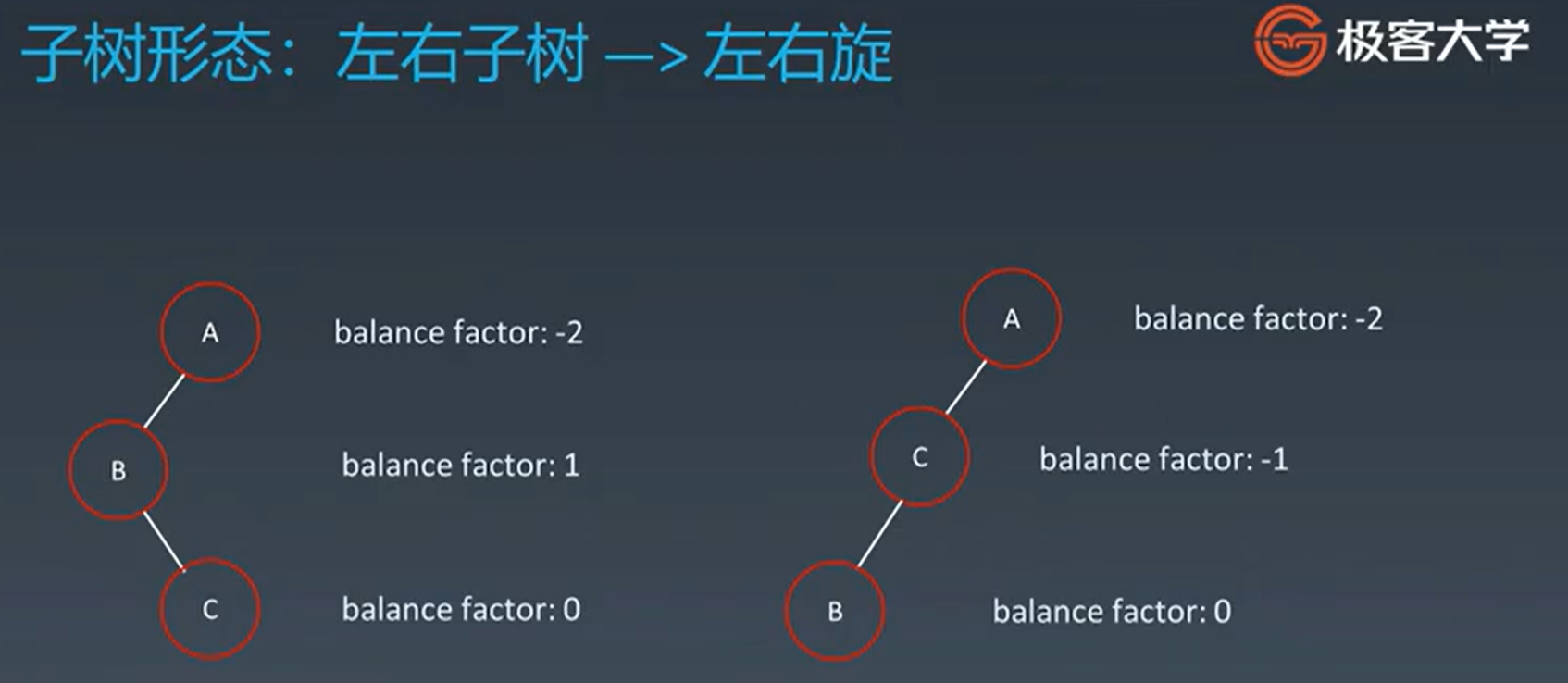
4,右左旋

红黑树(Red-black Tree)
红黑树是一种近似平衡的二叉搜索树(Binary Search Tree),它能够确保任何一个结点的左右子树的高度差小于两倍。具体来说,红黑树是满足如下条件的二叉搜索树:
- 每个结点要么是红色,要么是黑色;
- 根结点是黑色;
- 每个叶结点(NIL结点、空结点)是黑色的;
- 不能有相邻的两个红色结点;
- 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
- 关键性质:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。
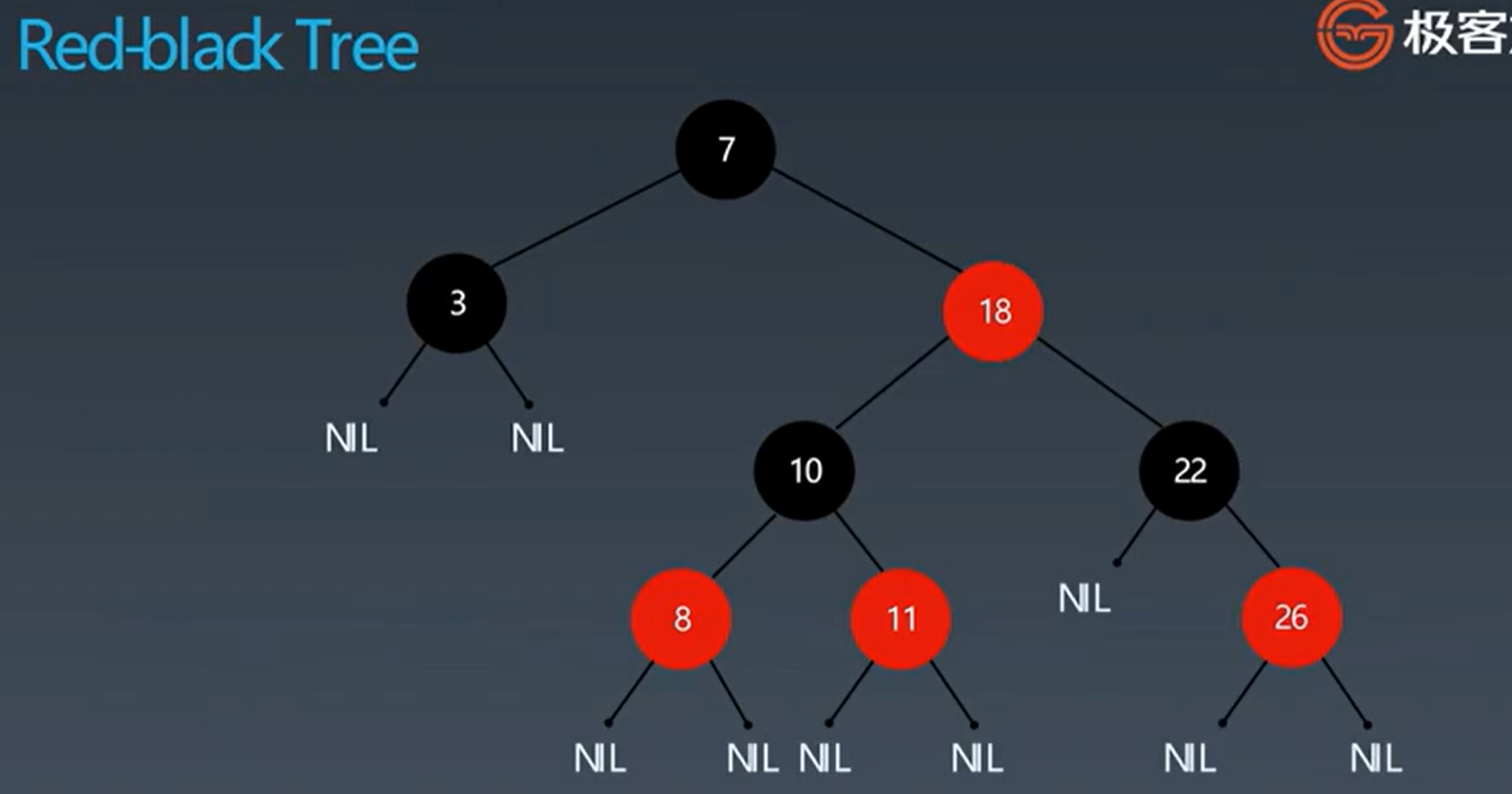
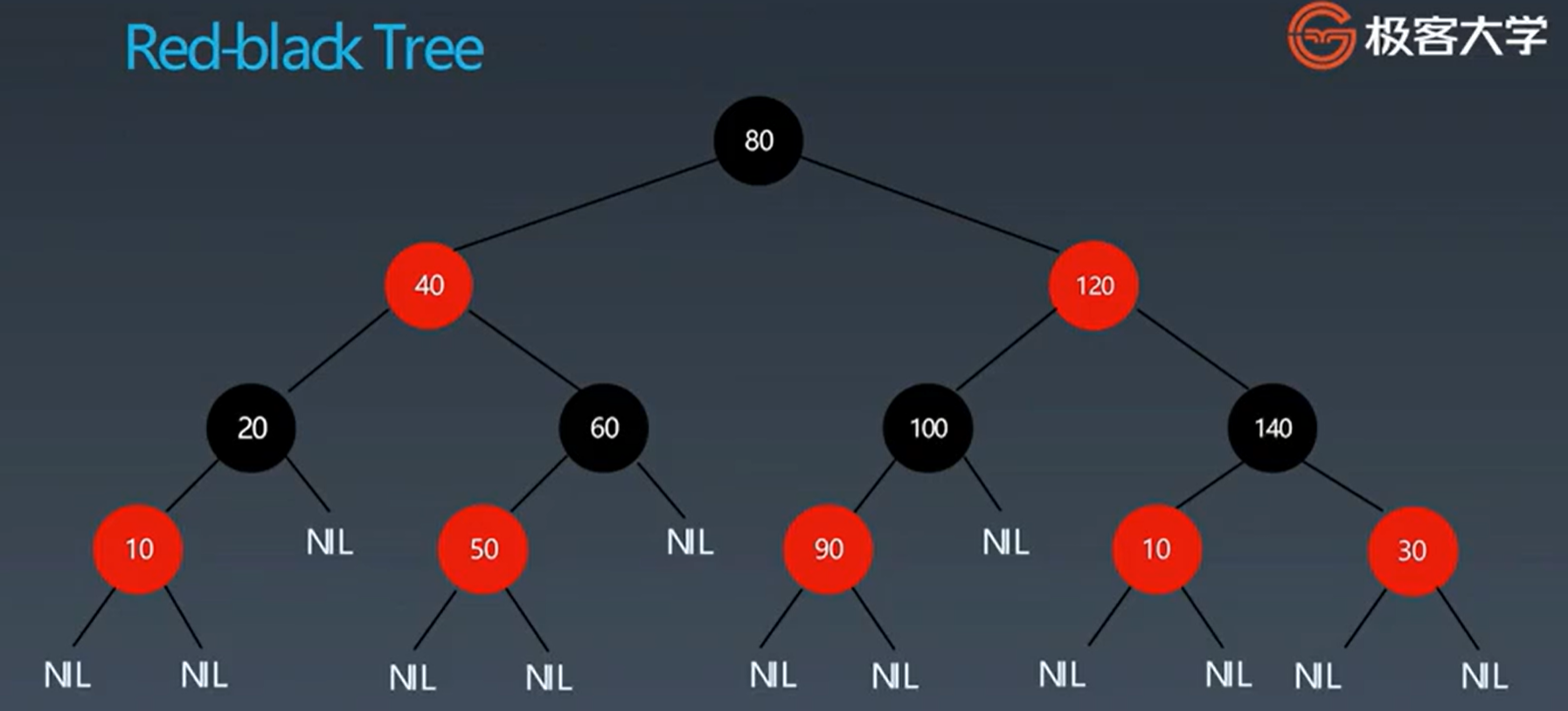
对比

翻译:
- AVL树提供了更快的查询,因为它是严格平衡的;
- 红黑树提供了更快的插入和删除的操作,因为AVL的旋转操作会更多而红黑树会更少一点;
- AVL存在
factors或heights更多一点,它需要更多的内存附加在每个结点里面来存这些了额外的信息,而红黑树要的信息非常少,它只要一个bit就是来存0和1表示黑或者是红; - 红黑树是用在你们常常写的一些高级语言的库里面,比如C++中的
map、set;如果用在数据库里面的话一般用AVL

