题目

力扣-剑指 Offer 07. 重建二叉树

知识点

二叉树的遍历顺序

1，前序（Pre-order）：根-左-右
2，中序（In-order）：左-根-右
3，后序（Post-order）：左-右-根

题解

解法一：递归

按题目给的示例来划分：
前序遍历划分 [ 3 | 9 | 20 15 7 ]
中序遍历划分 [ 9 | 3 | 15 20 7 ]

根据以上性质，可得出以下推论：

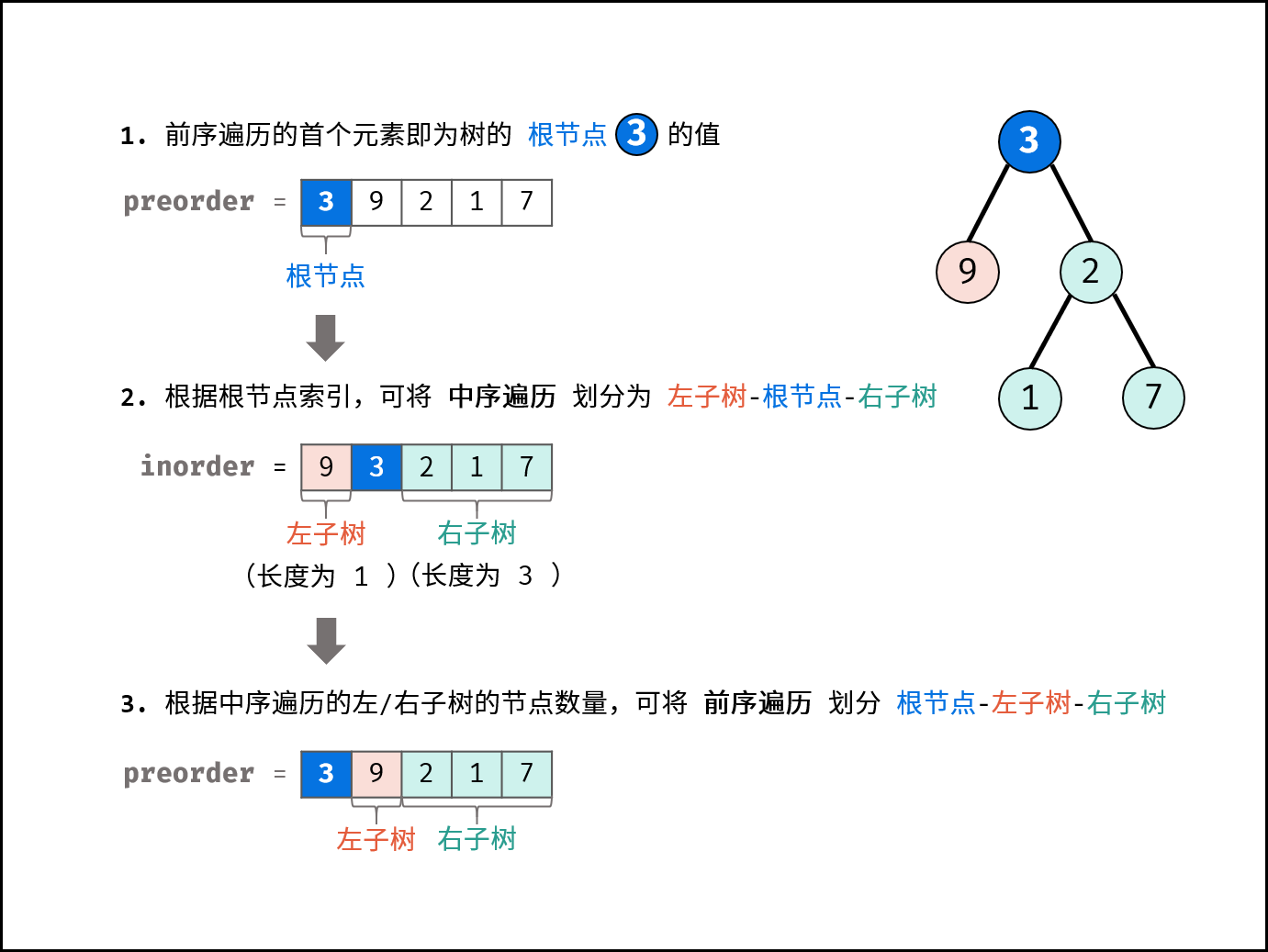
前序遍历的首元素为树的根节点 node 的值。
在中序遍历中搜索根节点 node 的索引，可将中序遍历划分为 [ 左子树 | 根节点 | 右子树 ] 。
根据中序遍历中的左 / 右子树的节点数量，可将前序遍历划分为 [ 根节点 | 左子树 | 右子树 ] 。

考虑通过递归对所有子树进行划分：

递推参数：根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right ；
终止条件：当 left > right ，代表已经越过叶节点，此时返回 null ；
递推工作：
建立根节点 node ：节点值为 preorder[root] ；
划分左右子树：查找根节点在中序遍历 inorder 中的索引 i ；

网上摘的保姆式的注解

//Java借助Map版本 (Go的没写出来，等后面写出来了再更新)
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
    int[] preorder;//保留的先序遍历，方便递归时依据索引查看先序遍历的值

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        this.preorder = preorder;
        //将中序遍历的值及索引放在map中，方便递归时获取左子树与右子树的数量及其根的索引
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        //三个索引分别为
        //当前根的的索引
        //递归树的左边界，即数组左边界
        //递归树的右边界，即数组右边界
        return recur(0,0,inorder.length-1);
    }

    TreeNode recur(int pre_root, int in_left, int in_right){
        if(in_left > in_right) return null;// 相等的话就是自己
        TreeNode root = new TreeNode(preorder[pre_root]);//获取root节点
        int idx = map.get(preorder[pre_root]);//获取在中序遍历中根节点所在索引，以方便获取左子树的数量
        //左子树的根的索引为先序中的根节点+1 
        //递归左子树的左边界为原来的中序in_left
        //递归右子树的右边界为中序中的根节点索引-1
        root.left = recur(pre_root+1, in_left, idx-1);
        //右子树的根的索引为先序中的 当前根位置 + 左子树的数量 + 1
        //递归右子树的左边界为中序中当前根节点+1
        //递归右子树的有边界为中序中原来右子树的边界
        root.right = recur(pre_root + (idx - in_left) + 1, idx+1, in_right);
        return root;

    }
}

leetcode-cn执行：

执行用时：
3 ms, 在所有 Java 提交中击败了55.11%的用户
内存消耗：
38.4 MB, 在所有 Java 提交中击败了80.00%的用户

//Go，不借助Map版本
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
    root := new(TreeNode)
    if len(preorder) == 0 {
        return nil
    }
    root_val := preorder[0]
    i := 0
    for inorder[i] != root_val {
        i++
    }
    left_tree := buildTree(preorder[1:i+1],inorder[:i])
    right_tree := buildTree(preorder[i+1:],inorder[i+1:])
    root.Val = root_val
    root.Left = left_tree
    root.Right = right_tree
    return root
}

leetcode-cn执行：

执行用时：
4 ms, 在所有 Go 提交中击败了95.75%的用户
内存消耗：
4.2 MB, 在所有 Go 提交中击败了25.36%的用户

牛客网运行：

运行时间：5ms
超过39.31%用Go提交的代码
占用内存：2344KB
超过9.75%用Go提交的代码

思考：为什么二叉树的题目一般用递归来解？

参考链接

4种解法（递归，栈，队列），最后一种击败了100%的用户
 力扣官方题解
 【面试题】重建二叉树（解题思路分析+Java、Python实现+代码详细注释）
面试题07. 重建二叉树（递归法，清晰图解）