栈与单调栈：最大矩形面积

任务

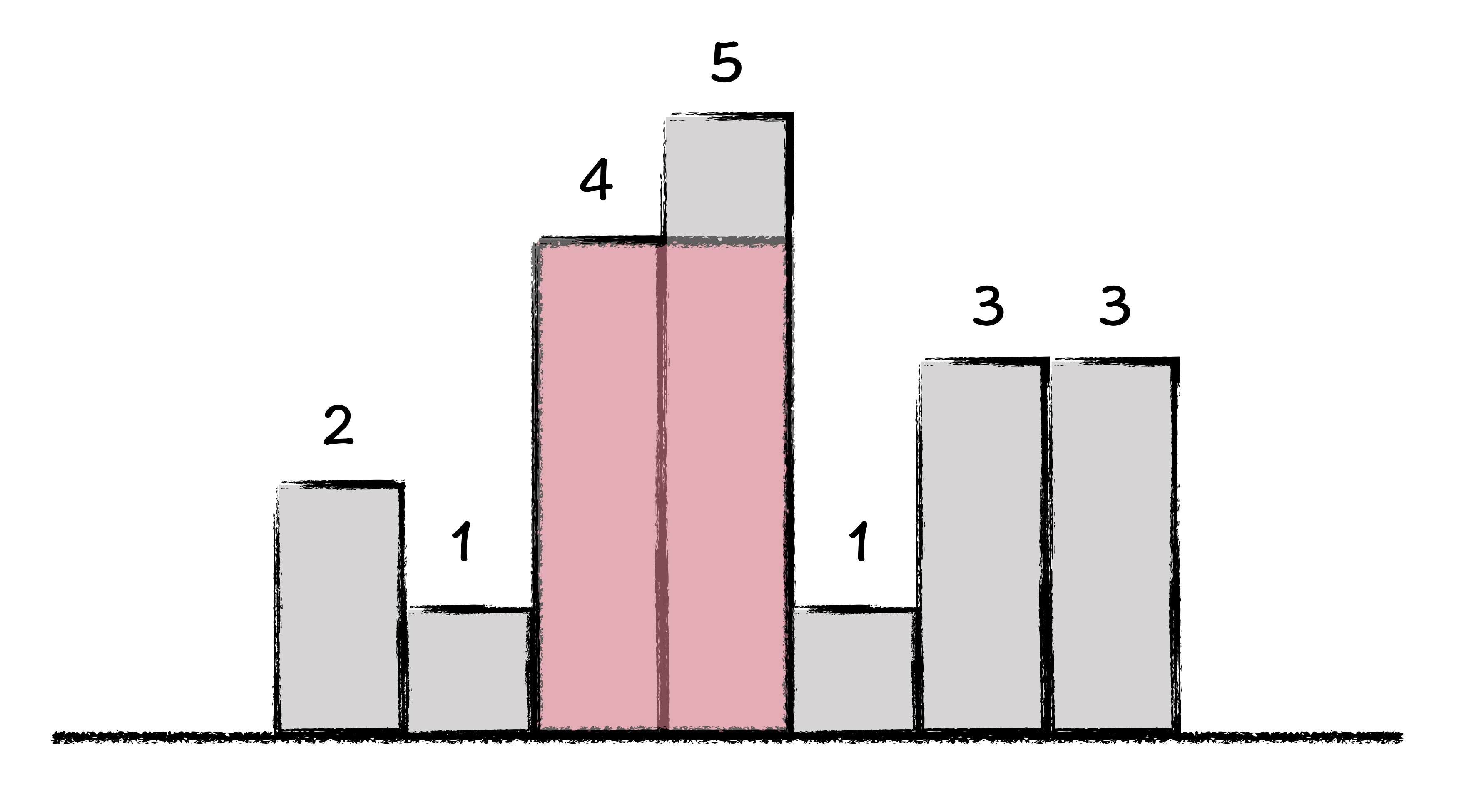
假设有一面木板墙，每块木板的宽度都是 1，你现在想在木板墙上，沿着平行于地面的方向，切割出一块矩形区域。问题来了，如果给出了每一块木板的高度，那么如何切出面积最大的矩形区域？矩形木板墙如下图所示：

思考

图中有 7 块木板，每块木板的高度分别为：2、1、4、5、1、3、3。经过尝试，我们发现最大矩形就是红色阴影部分所示，也就是切割了高度为 4 和 5 两块木板，形成了一个高度为 4，宽度为 2 的矩形区域，这个最大面积为 8。

结论：切下来的最大的矩形，一定是以最大矩形所在区域最短那块木板作为其高度值。

因此，可以枚举每一块木板，每次都以当前木板作为高度，就是把当前这块木板，当成是切出来的矩形区域中的最矮的木板，然后向左边和右边分别做延伸，切出此时的最大矩形区域。当把所有木板都试过一遍后，我们在所有枚举结果中比较出最大值，这个最大值就是我们要求的最大矩形面积。如果木板的个数为 n，那这种做法的时间复杂度接近于 O(n2)。

任务要求：将这个时间复杂度降低到 O(n)。

编码实现

栈：维护一种完全包含关系的结构

栈就是一种后进先出的结构。

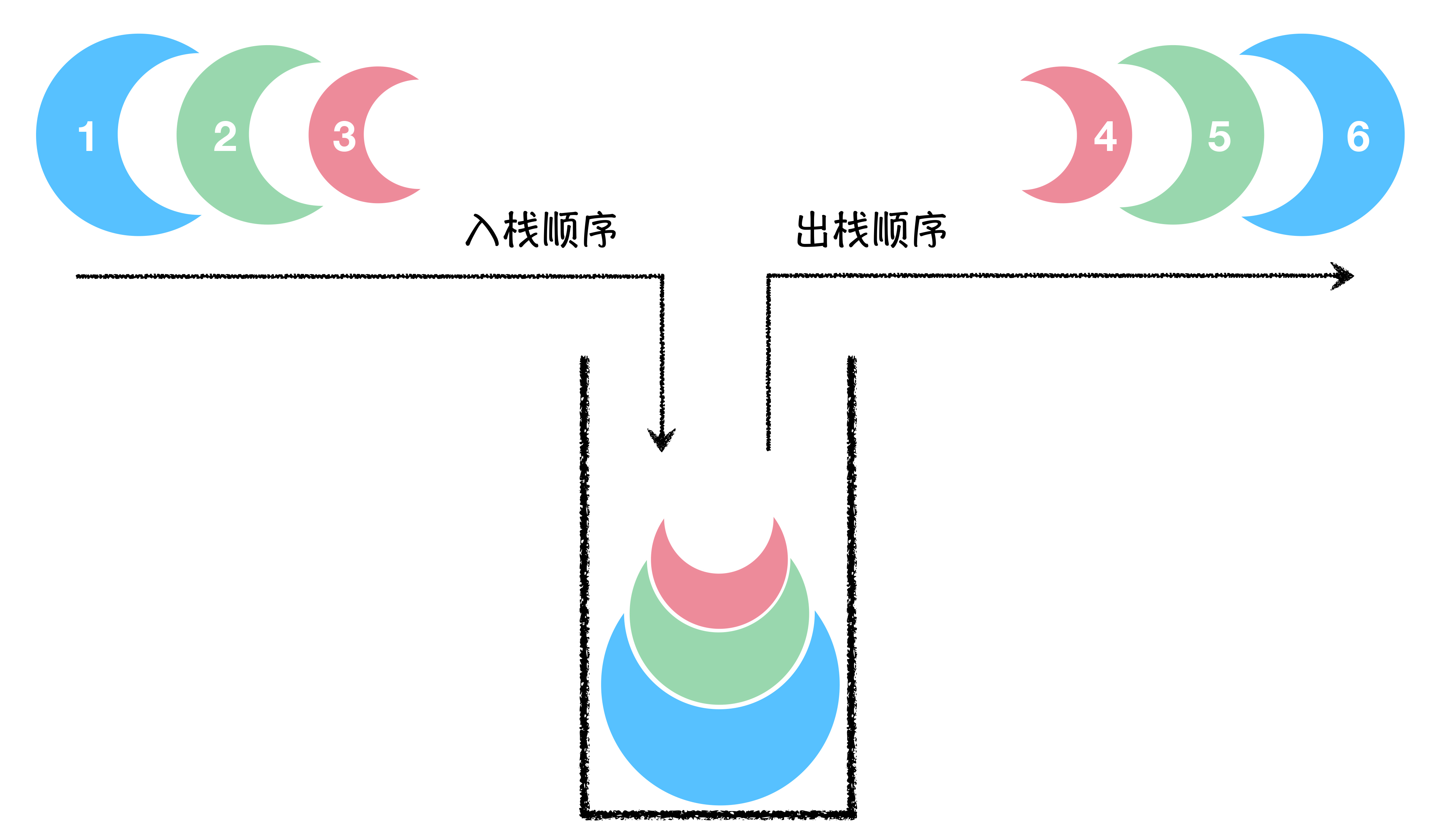
图中所示，入栈顺序分别是蓝、绿、红，那么出栈顺序就一定是红、绿、蓝。图中每一个颜色的方块上标注的数字，就是每一个方块入栈及出栈的顺序。

从示意图中，我们还可以观察到一个有趣的事情，在顺序上而言，红色方块被绿色方块包裹着，绿色方块被蓝色方块包裹着。这种结构，像是程序的调用过程，如果把蓝色方块，看成是主函数的话，那么绿色方块就是主函数中调用的一个函数 A，红色方块就是 A 函数中调用的另外一个函数 B，三个函数调用的顺序是主函数、函数 A、函数 B。
而它们的执行结束顺序恰恰是相反的，首先是函数 B 结束，然后是函数 A 结束，最后是主函数结束。

单调栈

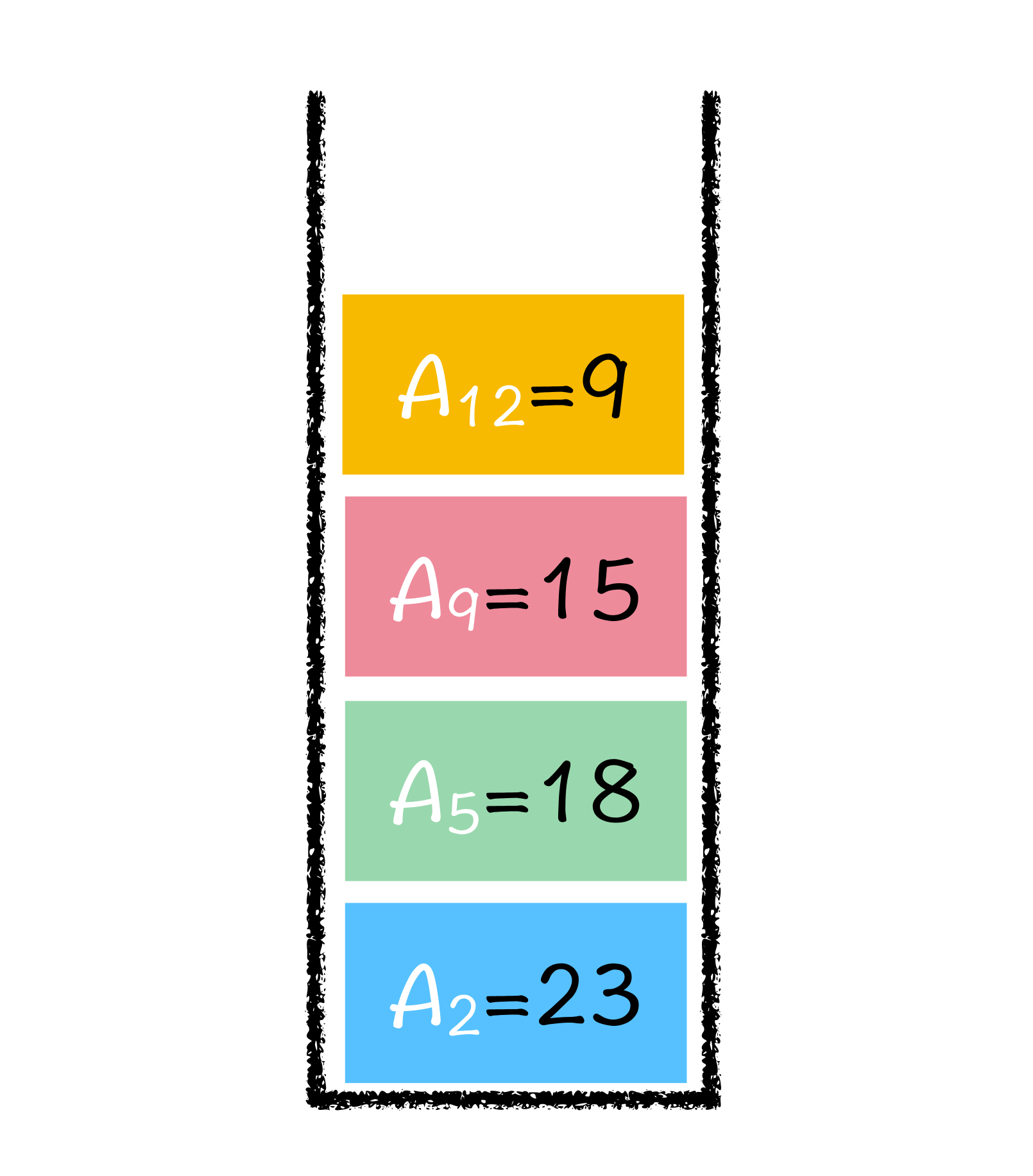
如果说单调队列是维护区间最值的高效结构，单调栈就是维护最近大于或小于关系的高效结构。

最大矩形面积

#define MAX_N 1000
#define max(a, b) ((a) > (b) ？ (a) : (b))
int s[MAX_N + 5], top;
int l[MAX_N + 5], r[MAX_N + 5];
int max_matrix_area(int *h, int n) {
    h[0] = h[n + 1] = -1;
    top = -1, s[++top] = 0;
    // 找到每一块木板，左边第一块比其矮的木板编号
    for (int i = 1; i <= n; i++) {
        while (top >= 0 && h[s[top]] >= h[i]) --top;
        l[i] = s[top];
        s[++top] = i;
    }
    // 找到每一块木板，右边第一块比其矮的木板编号
    top = -1, s[++top] = n + 1;
    for (int i = n; i >= 1; i--) {
        while (top >= 0 && h[s[top]] >= h[i]) --top;
        r[i] = s[top];
        s[++top] = i;
    }
    // 在所有木板中，找到面积最大的矩形
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, (r[i] - l[r] - 1) * h[i]);
    }
    return ans;
}

注意：代码中假设木板的编号是从 1 到 n 的，然后，在数组的 0 位及 n + 1 位分别加入两块高度为 -1 的虚拟木板，这是边界控制的一种技巧。也就是说，在每块木板向左搜索的时候，最远也就搜索到 0 号位就停止了，向右搜索的时候呢，最远搜索到 n + 1 位也就停止了。

通过加入虚拟木板，代码中就少了相关的边界条件判断，这是一种很实用的技巧。

小结

单调栈是用来维护最近大于或小于关系的数据结构。
单调栈就是堵住出口的单调队列，所以其时间复杂度与单调队列一致，平均到每个处理元素上，都是 O(1) 的时间复杂度。