深入理解：容斥原理与递推算法

任务

众所周知，在不计算小于 1 元钱的面额的前提下，我国的纸币系统中，曾经拥有如下面值：1 元、2 元、5 元、10 元、20 元、50 元和 100 元。假设，每一种面值的纸币，我们都有无限张，现在想用这些钱凑出 1000 元，请问你有多少种不同的方案？

这里说的不同方案，是不关注钱币之间的顺序的，例如要凑 7 元钱，可以是 1 元、5 元、1 元，也可以是 1 元、1 元、5 元，这两种方案我们视为同一种。

编码实现

容斥原理

一般在计数问题中，为了保证计数准确，必须注意两个事情：一是没有重复，二是没有遗漏。

容斥原理的基本思想：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排除出去，使得计算的结果既无遗漏又无重复。简单来说，就是在计算过程中，如果加多了，就把加多的部分减掉，如果发现又减多了，就再加回来一部分，一直到不多不少为止。

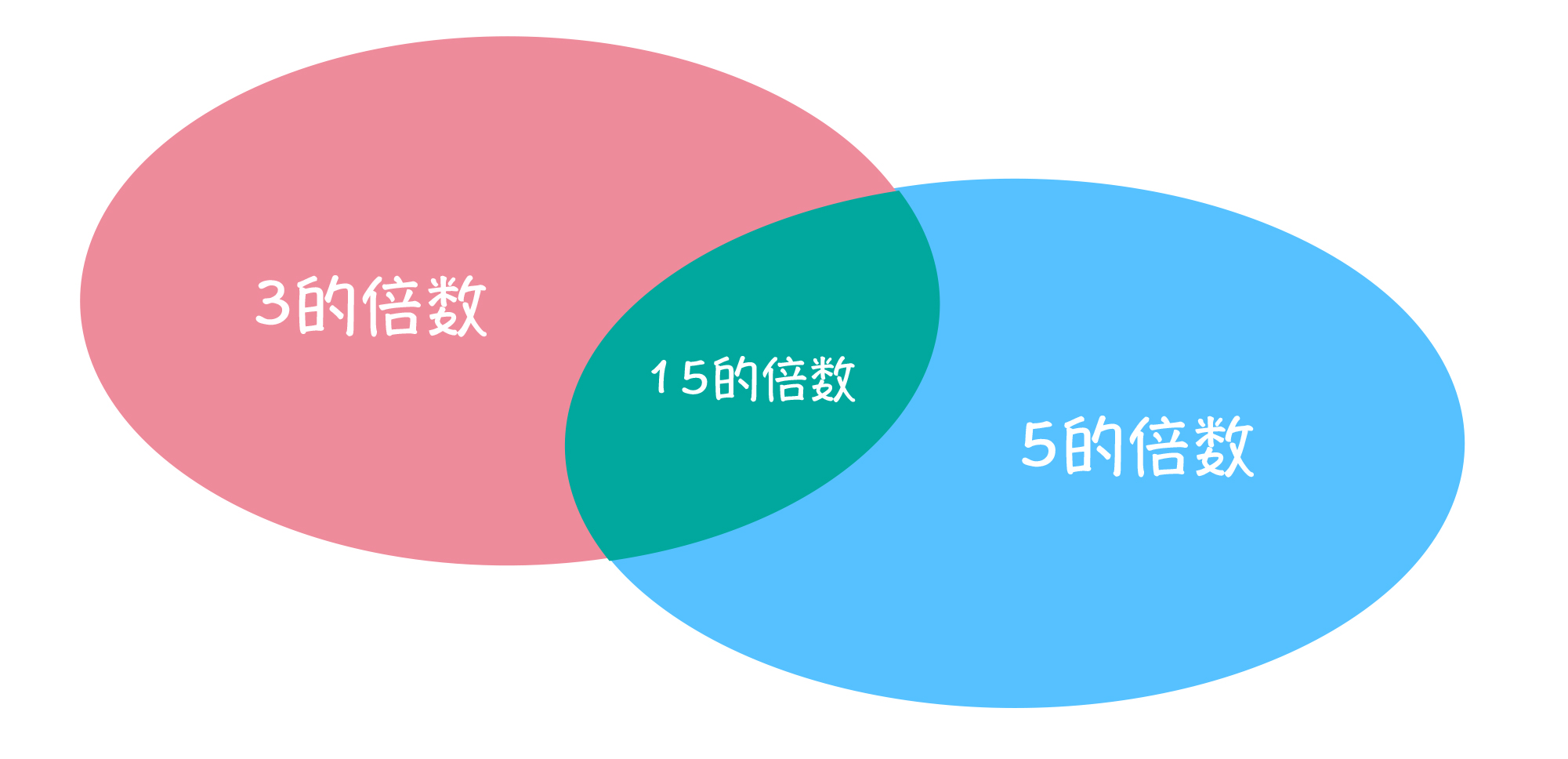
例如，求 1000 以内，3 或者 5 倍数的所有数字和的问题：

一个递推算法例子：兔子繁殖问题

假设在一片草原上，莫名其妙来了一只外星兔子，这种外星兔子呢，第一个月的时候是幼体，第二个月成长为成体，从第三个月开始，成体兔子每个月都会产生出一只克隆体的幼体兔子，而且这种兔子不会衰老，一旦成体以后，就会一直生下去。按照这种情况，请你计算出第 n 个月，草原上有多少只兔子？

给出前 6 个月，草原上兔子数量的情况：

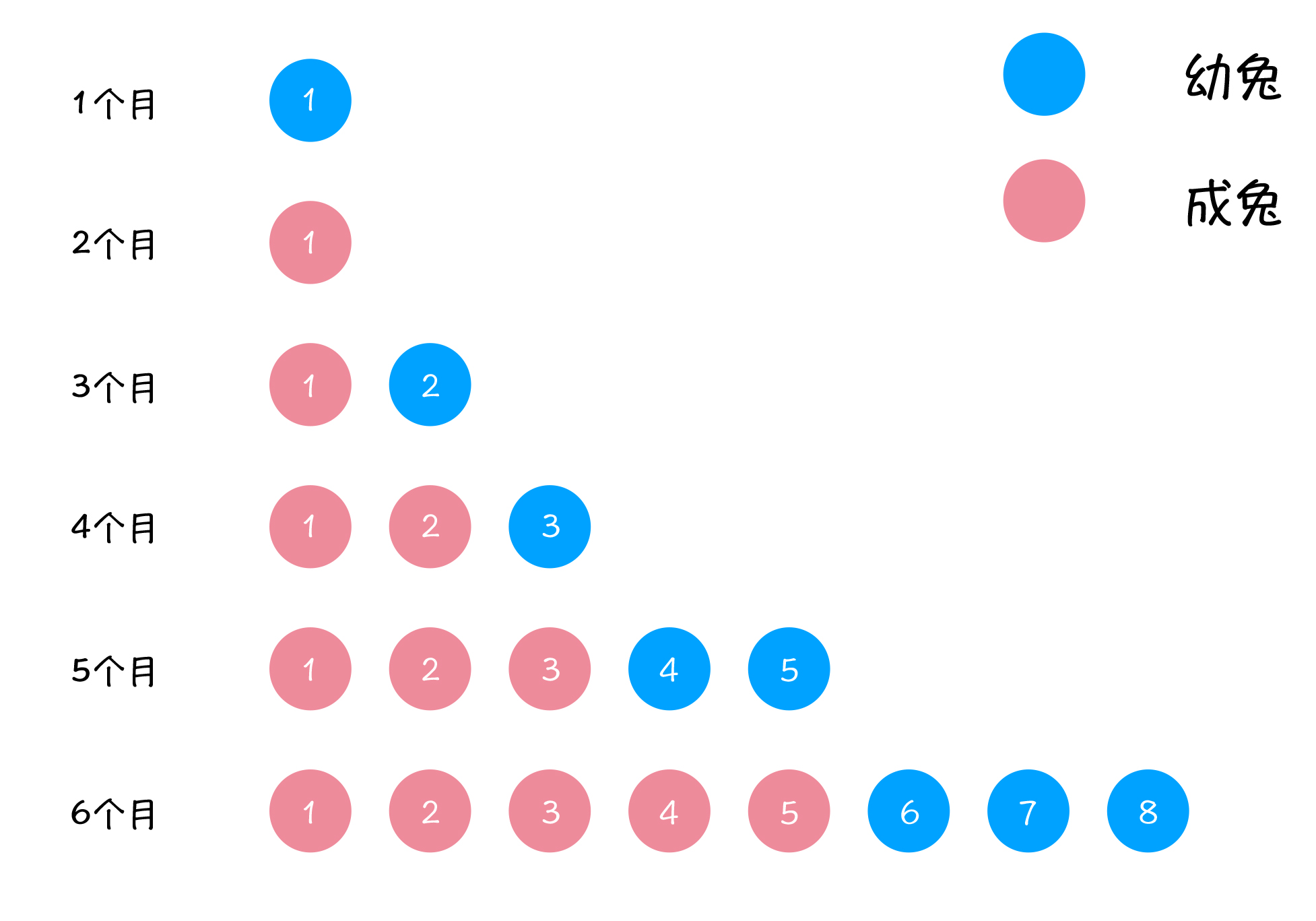
第6个月的兔子数量与前两个月兔子数量关系：

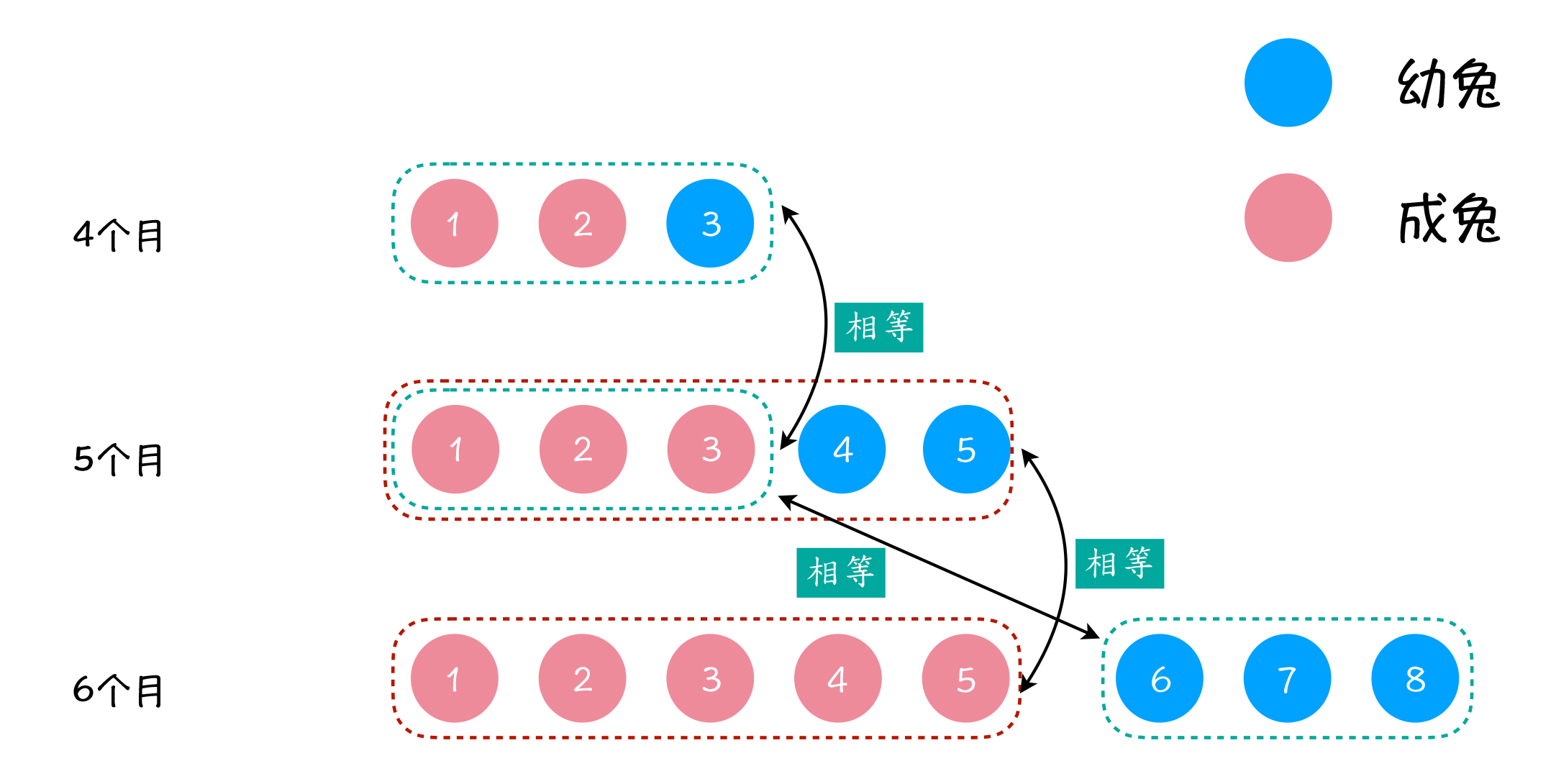
由于：第 6 个月的成兔数量等于第 5 个月的兔子总数，第 6 个月的幼兔数量等于第 4 个月的兔子总数，因此可以得出这样的一个结论：第 n 个月的兔子总数，等于该月的成兔数量与幼兔数量之和，也就等于第 n - 1 个月的兔子数量与第 n - 2 个月的兔子数量之和。

递推问题求解步骤，以兔子繁殖问题为例

递推问题，通常分成三步进行求解。第一步，确定递推状态，也叫做状态定义；第二步，推导递推公式；最后一步，程序设计与编写。

确定递推状态

确定一个有明确含义的数学符号，这里重要的是这个明确含义，而非那个数学符号。

先分析问题中的自变量和因变量。自变量，就是问题中那些不受控制的量，就像兔子繁殖问题中的月份。而因变量就是那些随自变量改变而改变的量，就像兔子繁殖问题中兔子的数量，是随着月份而改变的。

所以，我们把和问题求解量相关的自变量，都作为数学符号中的参数，然后将相关问题求解量作为数学符号映射值。f(n)代表第n个月兔子的数量，在这个状态定义中，将问题求解量，也就是兔子数量，作为函数映射值的含义；而与问题求解量，即兔子数量相关的自变量只有一个，那就是月份，所以我们将月份作为函数的参数。

推导递推公式

在推导递推公式的时候，这里需要用到前面我们定义的递推状态，并且，使用时一定要严格遵守递推状态的语义信息。

例如，在兔子繁殖问题中，如果你想用状态 f(n) 做公式推导的时候，那么 f(n - 1) 就代表了第 n - 1 个月兔子的数量，而 f(n - 2) 就代表第 n - 2 个月兔子的数量。

一般做递推公式推导的时候，我们主要思考的事情是，当前递推状态和前几项递推状态之间的关系。例如，在兔子繁殖问题中，当我们确定了递推状态 f(n) 以后，通过分析可以得到如下递推公式：

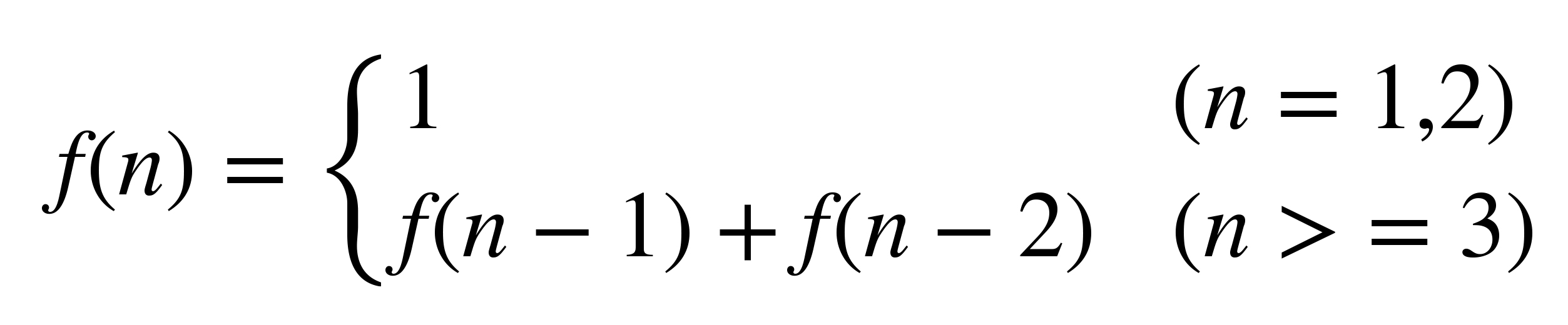
程序设计与编写

1，使用循环的程序实现方式

int cal_rabbit_num_loop(int n) {
    if(n == 1 || n == 2) {
        return 1;
    }
    int n1 = 1;
    int n2 = 1;
    int n3 = 0;
    for(int i = 0; i < n - 2; i++) {
        n3 = n1 + n2;
        n1 = n2;
        n2 = n3;
    }
    return n3;
}

2，使用递归的程序实现方式

int cal_rabbit_num(int n) {
    if(n == 1 || n == 2) {
        return 1;
    }
    return cal_rabbit_num(n - 1) + cal_rabbit_num(n - 2);
}

凑钱币问题解决

第一步，让我们来确定递推状态。确定递推状态之前，我们需要分析清楚题目中的自变量与因变量。因变量比较好分析，就是方案总数，那这个方案总数都受什么影响呢？很明显，是钱币的种类和拼凑目标金额。也就是说，钱币种类发生变化，方案总数就会发生变化；同理，如果拼凑的目标金额发生变化，方案总数也一定会发生变化。所以，自变量是 2 个，钱币种类和拼凑的钱币数量。因变量是 1 个，就是方案总数。通过上面的分析，我们就可以列出状态定义：f(i, j) ，代表使用前 i 种钱币，拼凑 j 元钱的方案总数。例如，f[3][10] 就代表使用前 3 种钱币，也就是只使用 1 元、2 元、5 元，凑 10 元钱的方案总数。
通过上面的分析，我们就可以列出状态定义：f(i, j) ，代表使用前 i 种钱币，拼凑 j 元钱的方案总数。例如，f[3][10] 就代表使用前 3 种钱币，也就是只使用 1 元、2 元、5 元，凑 10 元钱的方案总数。
第二步，就是用这个状态定义，进行递推公式推导，关键就是分析当前项与前几项的关系。核心思想其实就是容斥原理，也就是用某几项表示 f(i, j) ，如果发现这些表示 f(i, j) 的项之间存在交集，就将交集部分减去，如果减多了再加回来一些，直到正好表示 f(i, j) 为止。
好在这道题目还算是一道简单的递推问题，我们可以将 f(i, j) 划分成性质不同且互为补集的两部分。在 f(i, j) 所代表的所有方案中，一部分方案是使用了第 i 种钱币的，另外一部分方案中是没有使用第 i 种钱币的，我们就用这个性质，将 f(i, j) 表示成两项相加之和的形式。
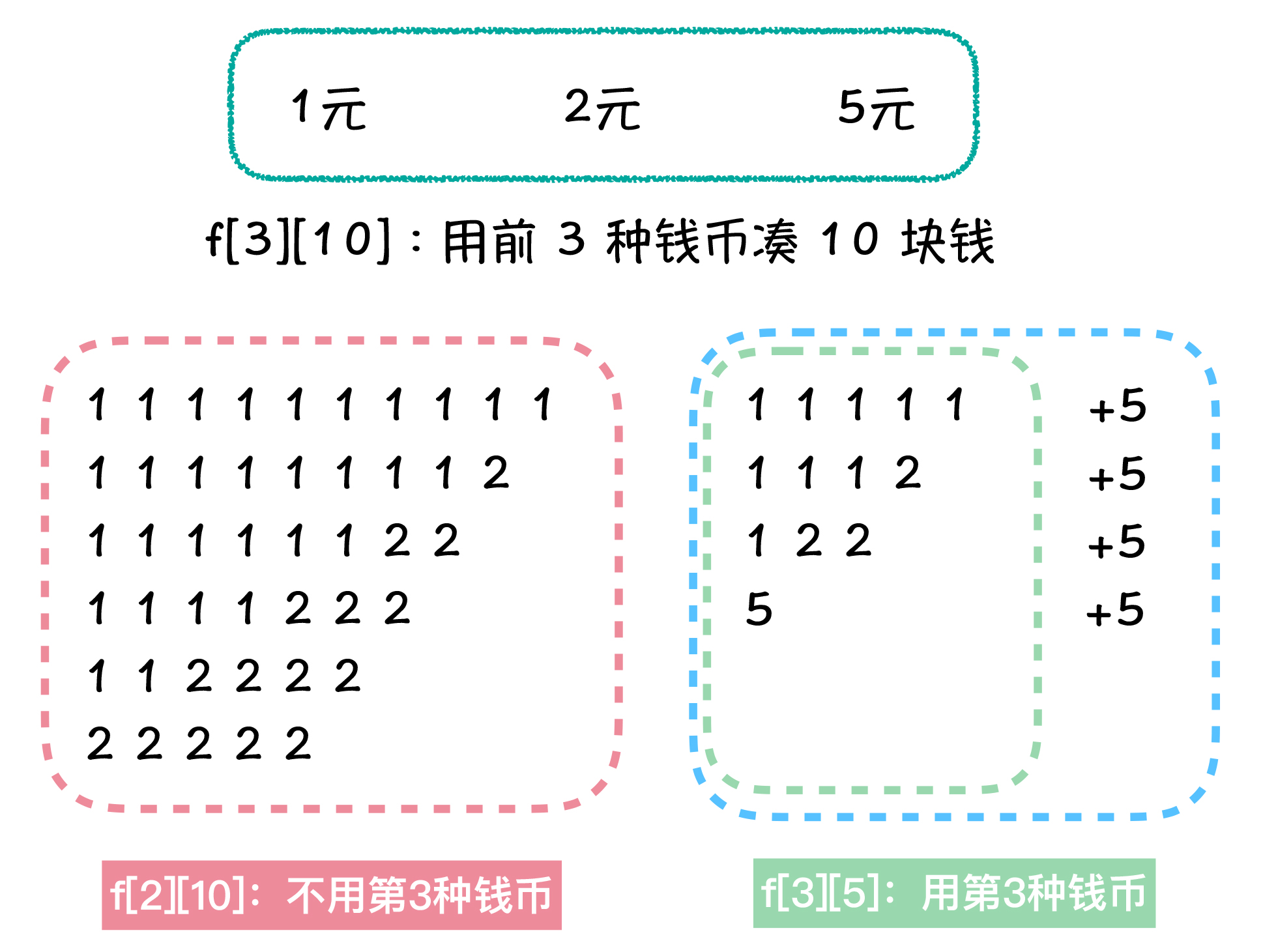
例如，在用前三种钱币，拼凑 10 元钱的所有方案中，可以按照方案中是否使用第 3 种钱币，也就是是否使用了 5 元钱，将所有方案划分成两类。
其中一类方案不包含第 3 种钱币，也就是不用 5 元这个钱币，这些方案的数量，等价于使用前 2 种钱币拼凑 10 元钱的方案总数，也就是 f[2][10] 的值。另外一类方案中，使用了至少 1 张 5 块钱，那么我们可以在这些方案中，都拿掉一张 5 元钱，剩余的部分组成的方案数量，就等于 f[3][5]，也就是用前 3 种钱币凑 5 元钱的方案总数。

这样我们就推导出了递推公式：f[3][10] = f[2][10] + f[3][5]。

在 f(i, j) 代表的所有方案中，没有使用第 i 种钱币，拼凑 j 元钱的方案数量，就是 f(i - 1, j)，代表使用前 i - 1 种钱币拼凑 j 元钱的方案总数。剩下的使用了第 i 种钱币的方案中，由于都存在第 i 种钱币至少 1 张，假设第 i 种钱币的面额是 val[i]，也就意味着，我们可以使用前 i 种钱币，凑 j - val[i] 的钱数，给第 i 种钱币留出一个位置，这么做所对应的方案总数就是 f(i, j - val[i])。

最终，我们推导出了递推公式：**f(i, j) = f(i - 1, j) + f(i, j - val[i])**。其中，边界条件是 f(1, k * val[1]) = 1，也就是用在只使用第 1 种钱币的条件下，想要凑第 1 种钱币的整数倍面额的方案总数都是 1。

int cal_coins(int i, int j) {
    if(j < 0) {
        return 0;
    }
    if(j == 0) {
        return 1;
    }
    if(i == 1 && j % val[1] == 0) {
        return 1;
    }
    return cal_coins(i - 1, j) + cal_coins(i, j - val[i]);
}
int main() {
    int n;
    scanf("%d", &n);
    printf("%d\n",cal_coins(3, n));
    return 0;
}

(有bug，待修正)

小结

递推问题第一步是要确定递推状态，也就是给出一个数学符号，以及数学符号的相关描述。
在设计递推状态的时候，主要分析自变量与因变量的关系，一般因变量都是问题求解的那个量。
递推问题的第二步是推导递推公式，而容斥原理的思想，对于这一步的求解，十分重要。