动态规划：只需四步，搞定动态规划算法设计

任务

数字三角形问题

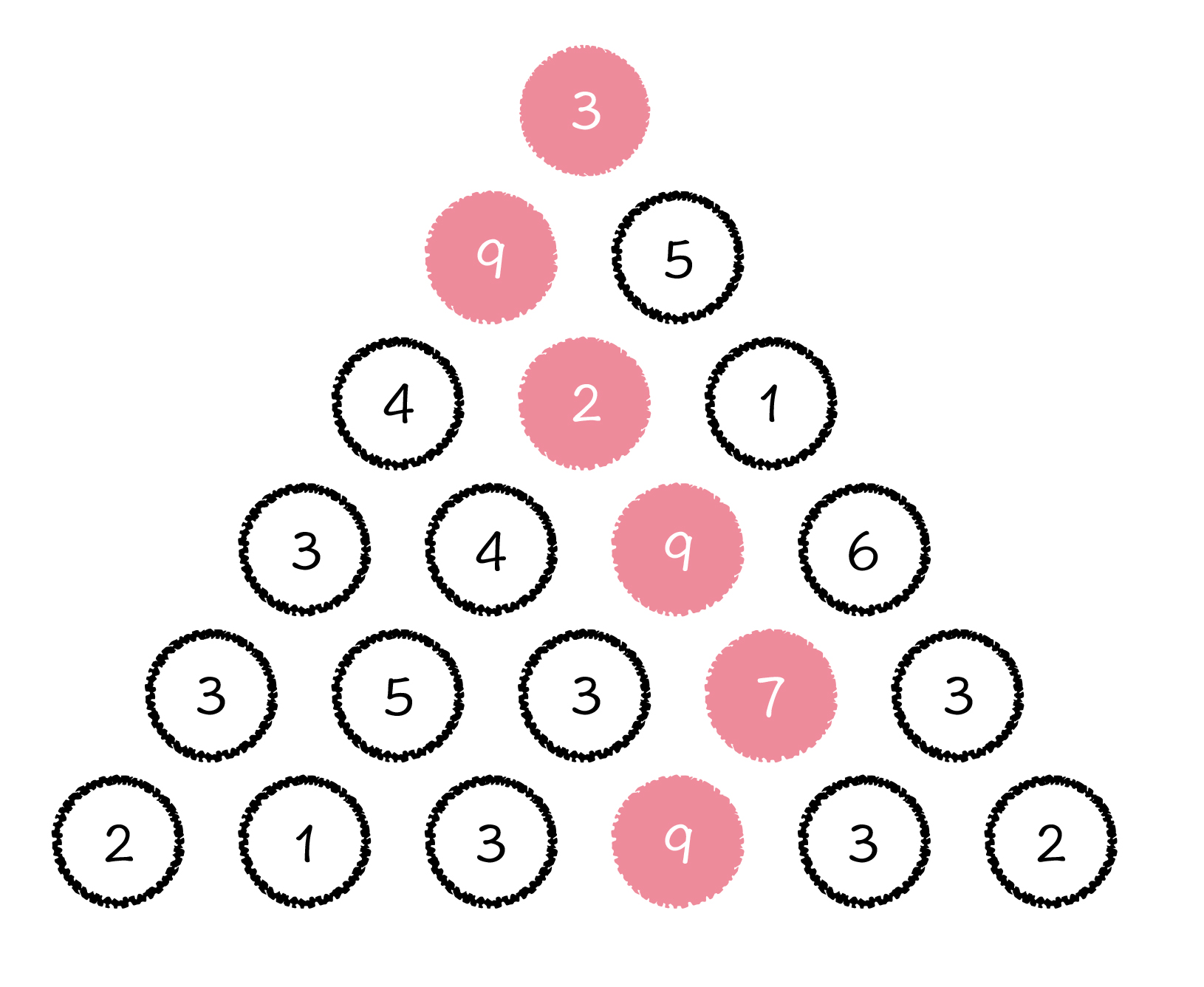
由上到下，第 i 层由 i 个数字组成，目标从第 1 层开始，每次只能向下走到相邻的两个节点，求走到最后一层路径上面数字的最大和值是多少。就像图中标红的一条线路，就是路径和值最大的一条路线，和值为 39。如果给你的是一个 n 层的数字三角形，你该如何解决这个问题呢？

数学归纳法思想

如果我们已知到第三层所有点的最大值，那么我们就可以计算得到起始点到第四层每一个的路径最大和值。所有绿色节点和蓝色节点，就是已经求出来的，起始点到其路径最大和值的点。其中的数字是根据上图中的数字三角形计算所得，比如第 2 层的 12，是由图 1 中第 1 层的 3 与原所在位置的 9，相加之和的结果。

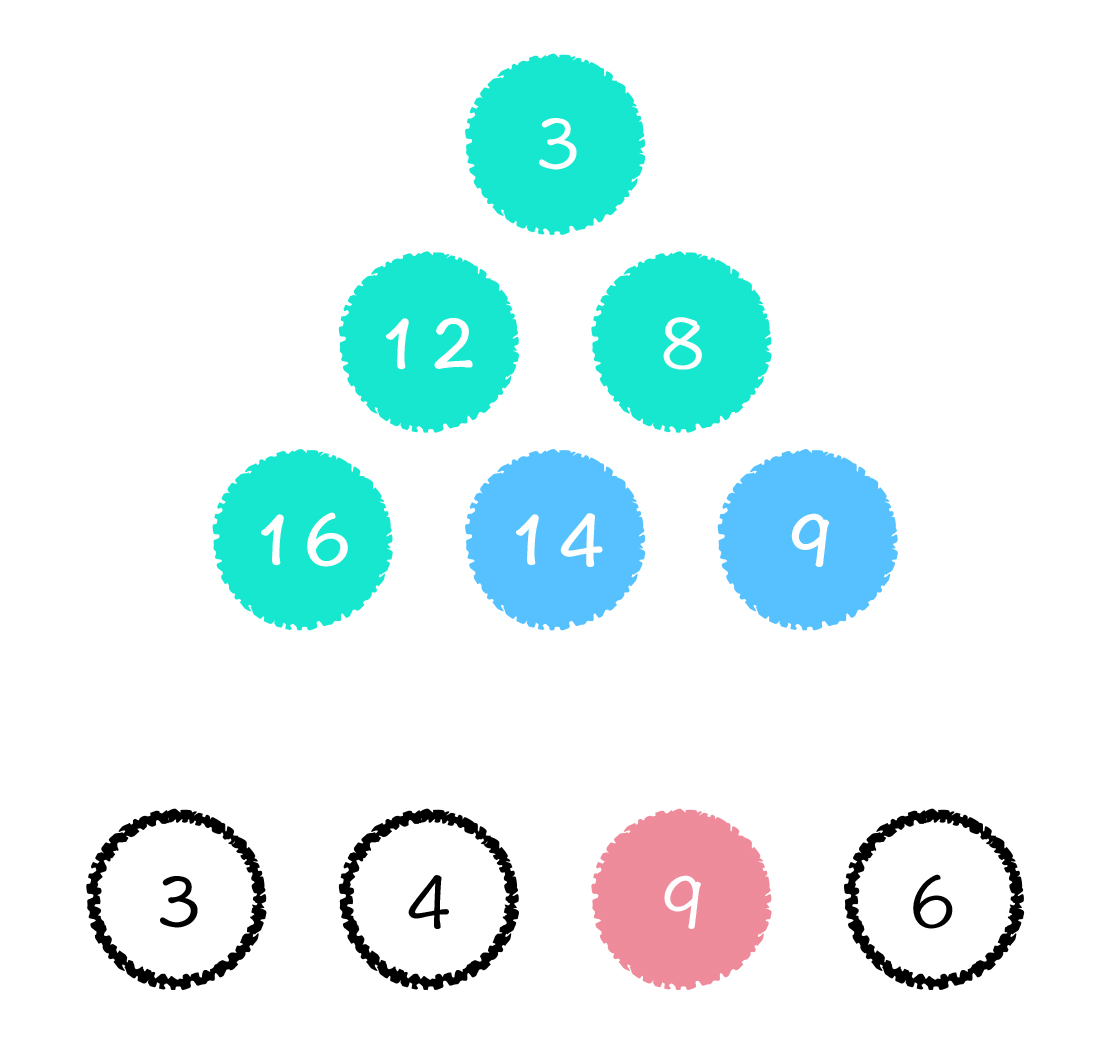
如果想求从起始点到红色的点，也就是第 4 行数字 9 点的路径最大和值，那么根据数字三角形的规则，我们只能从图中的两个蓝色点转移到红色点。那究竟选择从哪个点走到红色点呢？当然是选择其中和值较大的了，也就是从和值为 14 的点转移到红色点，得到的就是起始点到红色点的路径最大和值。

总结

若我们已知从起始点到第 i - 1 层上每个点的路径最大和值，那我们又是怎么得到从起始点到第 i 层上每个点的路径最大和值呢？请看下图：

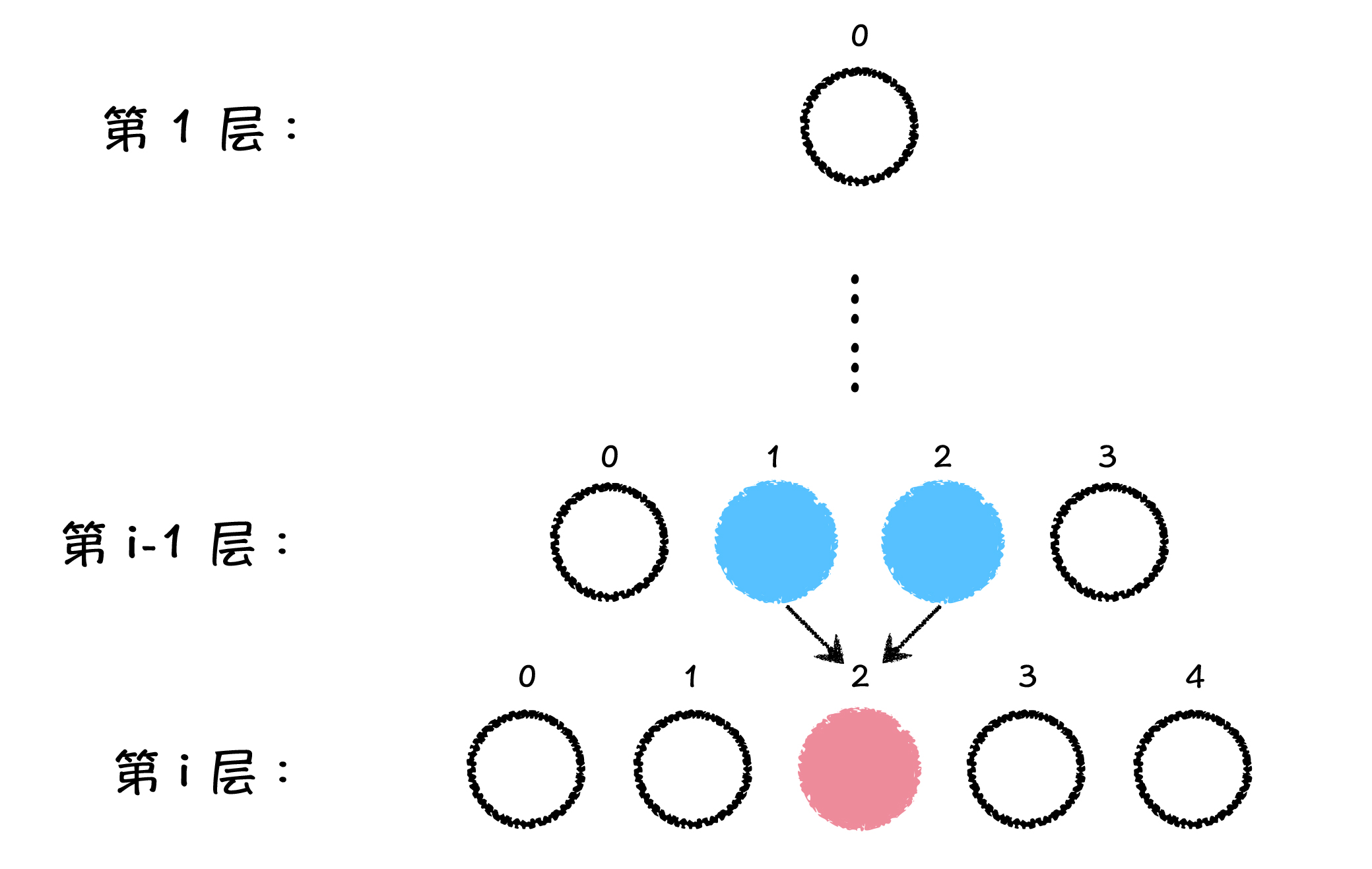
我们给每一层的节点，从左向右，从 0 开始依次编号，那么第 i 行的第 3 个点对应的坐标就是 (i, 2) 点。从第 1 层的点想要到达红色 (i, 2) 点，可以通过 (i - 1, 1) 点到达，或者通过 (i - 1, 2) 点到达。在已知从起始点到第 i-1 层上每个点的路径最大和值的前提下，从第 1 层到 (i, 2) 点的最大和值，就是在 (i - 1, 1) 和 (i - 1, 2) 这两个值中，选择一个路径和值最大的，然后转移到 (i, 2) 点，即为第 1 层到 (i, 2) 点的路径最大和值。

所以，我们基本可以确定一件事情了，如果我们要是知道第 1 层到 i - 1 层的每个点的路径最大和值，那就很容易求得到第 i 层每个点的路径最大和值，从而推导出 i + 1 层、i + 2 层等等的路径最大和值，直到最后一层。

又因为，我们已知第 1 层到第 1 层每一个点的路径最大和值，就是起始点原本的值，所以沿着上面这个思路，就可以按照层序，来求解第一层到每一层的每个节点的路径最大和值了。

动态规划算法的四步走

状态定义

理解一个动态归划问题的状态定义，是理解其解法的第一步，也是最重要的一步。如果你在往下进行推导的时候，发现进行不下去了，那往往就是状态定义有问题，这时你就需要回到这个第一步，琢磨琢磨新的状态定义了。

并且，我们一直在强调，对于动态规划的状态定义，不仅仅是要一个数学符号，还要一个明确的语义信息，你的理解可能是：不同的语义信息，对应的不就是不同的数学符号么？那今天，我们就用同一个数学符号，表示不同的语义信息，在接下来的求解过程中，你会发现这两种不同的语义信息，所衍生出来的后续步骤过程，是完全不同的。

回到前面说的数字三角形问题，我们可以作出两种状态定义：

第一种状态定义：dp[i][j] 代表从起始点，到 (i, j) 点的路径最大值。
第二种状态定义：dp[i][j] 代表从底边的某个点出发，到 (i, j) 点的路径最大值。

为了后续讲解方便，我们假设所有坐标都是从 1 开始的，也就是第一行第一个点的坐标是 (1, 1)。你会发现，这两种状态定义，数学符号都是 dp[i][j]，而含义却完全相反，一个是从顶向下走，一个是从底向上走。对于第一种状态定义，如果数字三角形有 n 层的话，问题所求的最大值，就是在最后一层 dp[n] 中的某个值。而第二种状态定义，问题所求的最大值最终会存储在 dp[1][1] 这个状态值中。

状态转移方程

状态转移，就是状态之间的转移，每一个状态的含义，在状态定义中规定的明明白白，而状态与状态之间的转移方式，是需要根据具体的问题以及具体的状态定义，进行具体分析。

根据刚才作的两种状态定义，我们可以分别画出来这样两种状态转移的方向：

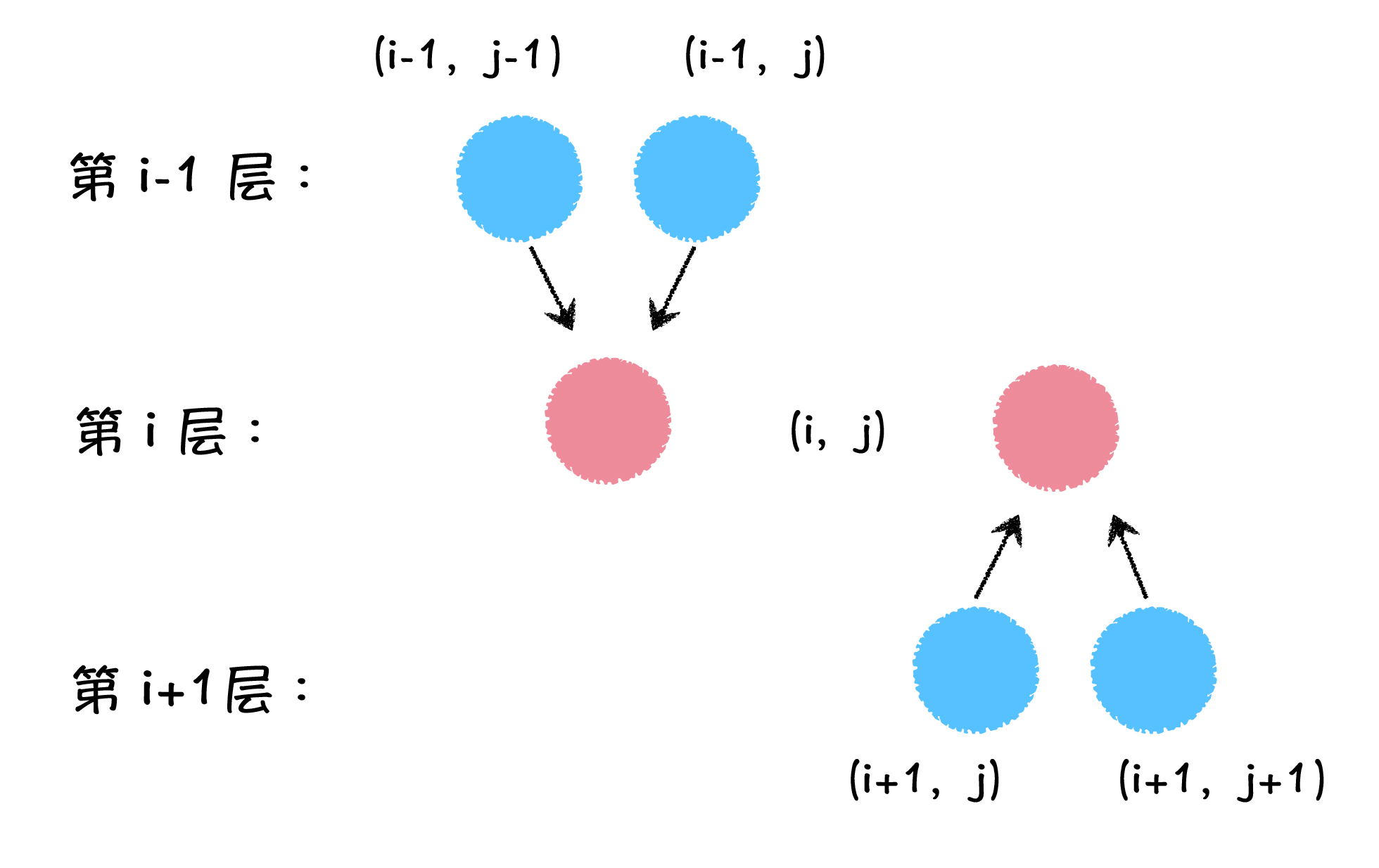
如图所示，我以左边是第一种状态定义下的状态转移方向为例，来说明它是如何转移的。首先，它是自上向下转移的，所以想要求得 dp[i][j] 的值，我们需要知道 dp[i - 1][j - 1] 和 dp[i - 1][j] 的值。因为按照“走向下个相邻两点”的规则，只有 (i - 1, j - 1) 和 (i - 1, j) 这两个点，才能能走到 (i, j)，也就是我们讲到的转移到 (i, j) 点。右边的第二种状态定义转移过程和左边的一样，只是移动方向不一样而已。

所以，根据两种状态定义，我们可以分别列出这两种状态转移方程：

第一种状态转移方程：dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + val[i][j]
第二种状态转移方程：dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + val[i][j]

两种转移方程，都是在能够转移到 (i, j) 点的状态值中选择一个较大值，再加上 (i, j) 原本的数值 val[i][j]，就是各自起始点到达 (i, j) 点的路径最大值，也就是两种状态定义下的 dp[i][j] 的值。

到这里，你可以看出，状态定义不一样，直接导致我们的状态转移方程就不一样。所以，虽然是相同的数学符号，定义的含义不同，就会造成后续的解法不同，同时也意味着解决问题的难度不同。

正确性证明

关于状态转移方程的正确性证明，借助的就是程序设计中最重要的数学思维：数学归纳法。

根据数学归纳法的三步走，我们试着证明一下第一种状态转移方程是正确的，也就是自上而下的状态转移方式。

第一步，我们已知在这种状态转移方式中，第一个阶段中的所有 dp 值都可以轻松获得，也就是可以很轻松的初始化 dp[1][1] 的值，应该等于 val[1][1] 的值。

第二步，我们假设如果第 i-1 阶段中的所有状态值，我们都正确的得到了。也就是正确的得到了从起始点到 i-1 层中每个点的路径最大和值。那根据状态转移方程：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j + 1]) + val[i][j] 来说，就可以正确的计算得到第 i 个阶段中的所有状态值。

第三步，两步联立，就可得出结论，所有阶段中的状态值计算均正确。那么，从起始点到底边的路径最大和值，就在最后一个阶段的若干个状态值中。

程序设计与实现

#include <stdio.h>
int main()
{
    int n, i, j;
    int s[50][50];
    int p[50][50];
    scanf("%d", &n);
    for(i = 1; i <= n; i++)
    {
        for(j = 1; j <= i; j++)
        {
            scanf("%d", &s[i][j]);
        }
    }
    for(j = 1; j <= n; j++)
    {
        p[n][j] = s[n][j];
    }
    for(i = n - 1; i >= 1; i--)
    {
        for(j = 1; j <= i; j++)
        {
            if(p[i + 1][j] > p[i + 1][j + 1])
            {
                p[i][j] = s[i][j] + p[i + 1][j];
            }
            else
           {
               p[i][j] = p[i + 1][j + 1] + s[i][j];
           }
        }
    }
    printf("%d\n", p[1][1]);
    return 0;
}

小结

状态定义，是动态规划算法的重点，无论是解题还是学习，都要从这一步开始。
不同的状态定义，决定了不同的状态转移方程，同时也可能代表了不同的解题难度，所以，学习如何定义优秀的状态很重要。
动态规划中的状态转移顺序，是建立在“阶段”概念之上的，只有本阶段的状态值计算完了，下一个阶段的状态值才能得以计算。
数学归纳法，是证明动态规划状态转移方程正确性的利器，掌握了它，会让你的动态规划学习过程事半功倍！